2022-2023八年级数学上册第11章11

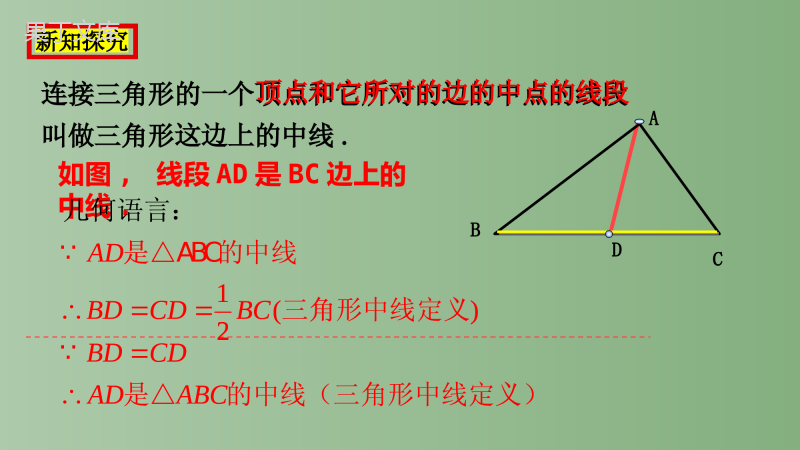
第十一章三角形11.1.2三角形的高、中线和角平分线第二课时人教版八年级上册晓老师课堂学习目标1.理解三角形的中线和角平分线的定义，会画出这两种重要的线段。2.了解三角形的中线和角平分线的性质，并能应用它来解决实际问题。3.解三角形的稳定性在日常生活中的应用线段中点的定义：线段上的一点把线段分成相等的两部分，这个点叫线段的中点知识回顾12CABACCBAB为中点几何语言：ACCBC为线几何语言：段的中点ABC12CABACCBAB为中点几何语言：ACCBC为线几何语言：段的中点连接三角形的一个顶点和它所对的边的中点的线段叫做三角形这边上的中线.如图,线段AD是BC边上的中线.ABCD新知探究顶点和它所对的边的中点的线段1()2ADBDCDBC是△A几何语BC的中线三角言形中线定义：BDCDADABC是△的中线（三角形中线定义）1()2ADBDCDBC是△A几何语BC的中线三角言形中线定义：BDCDADABC是△的中线（三角形中线定义）D任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?●●EFO三角形的三条中线相交于一点，这个交点叫做三角形的重心它在三角形的内部.新知探究ABC1.如图所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是()A.DE是△BCD的中线B.BD是△ABC的中线C.AD=DC,BE=ECD.CE=CDEDCBAD跟踪练习2．如图，若AD是△ABC的中线，BD=3，则CD的长度为（）A．2B．3C．4D．8B新知探究如图，若AD是△ABC的中线，说明S△ABD与S△ACD的大小关系E∟△ABD的底是BD时，高为AE,解：过点A作AEBC⏊与E△ACD的底是CD时，高为AE,∵AD是△ABC的中线∴BD=CD∴S△ABD=S△ACD（等底同高）结论：三角形的中线把三角形的面积分成相等的两部分如图、在△ABC中，点D、E分别是边BC、AB的中点，若△ABC的面积等于8，求△BDE的面积例题分析解：∵点D是BC中点4SABDSABC=81SABC2SABD∵点E是AB中点1SABD=22SBDE4SABDSABC=81SABC2SABD1SABD=22SBDE知识回顾三角形除了重要线段高线和中线以外，还有一条重要线段，不过先回顾相关的知识从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线。0ABC12AOCCOBAOBOCAOB平：分几何语言12OCAOBAOCBOCAOB是几何语言：的平分线12AOCCOBAOBOCAOB平：分几何语言12OCAOBAOCBOCAOB是几何语言：的平分线ABCD几何语言∵AD是△ABC的角平分线∴∠1=∠2=１２∠BAC●●三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段,叫做三角形的角平分线。角的顶点与交点之间的线段,︶︶12新知探究∵∠1=∠2=１２∠BAC∴AD是△ABC的角平分线任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?FEDO三角形的三条角平分线交于一点，交点在三角形内部动手操作ACB判断三角形角平分线可能在三角形外部（）三角形角平分线的交点在三角形外部（）××如图，已知AC平分∠EAG，BD平分∠FBG，∠1＝35°,∠2＝35°,那么直线AC与BD平行吗？直线AE与BF平行吗？例题分析解：AC∥BD，AE∥BF．理由如下：∵∠1=∠2=350∴AC∥BD∵AC平分∠EAG，BD平分∠FBG∴∠EAG=2∠1，∠FBG=2∠2∴∠EAG=∠FBG∴AE∥BF三角形的稳定性三角形具有稳定性，四边形具有不稳定性。窗框在未安装好之前，木工师傅常常先在窗框上斜钉一根木条，为什么要这样做呢？新知探究三角形的稳定性的应用四边形不稳定性的应用新知探究1.下列图形中具有稳定性的是（）（A）正方形（B）长方形（C）直角三角形（D）平行四边形C2.要使下列木架稳定各至少需要多少根木棍？跟踪练习（1根）（2根）（3根）1.如图，在ΔABC中，AE是中线，AD是角平分线，AF是高。填空：（1）BE==；（2）∠BAD==；（3）∠AFB==90°；12BACFEDCBACE∠CAD∠AFC当堂检测12BC12BAC12BC当堂检测1．如图，线段AD把△ABC分成面积相等的两部分，则线段AD是（）A．△ABC的中线B．△ABC的高C．△ABC的角平分线D．以上都不对A2．如图，在△ABC中，AB=15，AC=12，AD为中线．则△ABD与△ACD的周长之差为（）A．1B．2C．3D．4C当堂检测3.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B落在点B′的位置,则线段AC具有性质()A.是边BB′上的中线B.是边BB′上的高C.是∠BAB′的角平分线D.以上三种性质合一B'CBAD4．如图，在△ABC中，点D、E分别是BC、AB上的中点，连接AD、DE，若S△DEA=2，则四边形AECD的面积为（）A．7B．6C．8D．12B5．如图所示，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，则图中与阴影三角形面积相等的三角形（不包括它本身）有几个（）A．2B．3C．4D．5当堂检测D6.如图，在△ABC中，AD，AE分别是边上的中线和高，点D在点E的左侧，已知AE=4，DE=1，S△ABC=16，CE=（）A．2B．3C．4D．5B坚持就是胜利