1.5.1乘方,1.5.1乘方第二课时教案

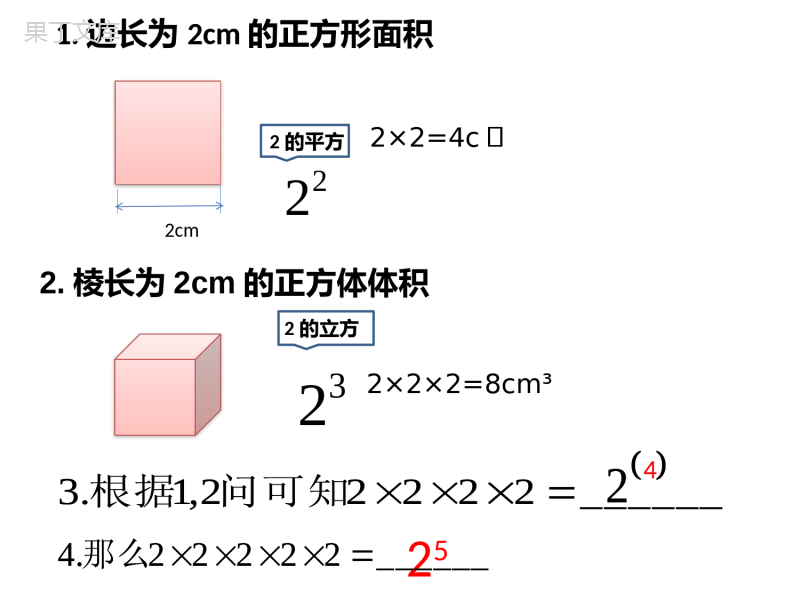
课前赠言：知己知彼，百战不殆。请拿出你的课本、导学案，双色笔，练习本，还有你的激情。温馨提示1.5有理数的乘方【学习目标】知识与技能：理解有理数乘方的意义,能正确进行有理数乘方的运算。过程与方法：通过对乘方意义的理解，培养观察比较、分析、归纳，概括的能力，渗透转换思想。情感态度与价值观：体会数学运算间的联系。【重点】正确理解乘方的意义，能利用乘方运算法则进行有理数乘方运算。【难点】准确理解底数，指数和幂三个概念，并能进行幂的运算。反映出的问题：失败带给我的经验与收获，在于我已经知道这样做不会成功的证明，下一次我可以避免同样的错误了。——爱迪生1.书写格式不规范2.不会写乘方形式3.不理解乘方表示的意义1.边长为2cm的正方形面积2×2=4c㎡2×2×2=8cm³2cm2的平方2的立方22322.棱长为2cm的正方体体积______22222,1.3问可知根据______22222.4那么2254______22222,1.3问可知根据______22222.4那么21.乘方：求n个相同因数的积的运算，乘方的结果叫做幂。34读作：3的4次方或3的4次幂表示：99个（-1）相乘读作：-1的99次方或-1的99次幂nan个naaaa991na底数指数幂一个数可以看作这个数本身的一次方33表示：n个a相乘表示：4个3相乘717读作：a的n次方或a的n次幂813333337178133332.计算（1）2×2×2×2=__________=_________（2）3×3×3=_______=___________（3）(-1)×(-1)×(-1)×(-1)=________=__________（4）(-2)×(-2)×(-2)=__________=__________（5）0×0×∙∙∙×0(2019个)=__________162427331(-1)4-8(-2)30通过以上运算发现什么规律？归纳：正数的任何次幂都是_______数；负数的奇次幂是_______数，负数的偶次幂是_______数；0的任何正整数次幂都是________.正正负0是什么数？思考：2a022aa是一个非负数，即非负数（或偶数次方）为一个任何一个数的偶数次幂是什么数？思考：2a022aa是一个非负数，即非负数（或偶数次方）为一个任何一个数的偶数次幂的值。求满足.例题若bababa,023,29.的值为所以解得：解：由题意得：b2ba93)(a2b3,a02b0,3a的值。求满足.例题若bababa,023,29.的值为所以解得：解：由题意得：b2ba93)(a2b3,a02b0,3a一样吗？为什么？与思考442)2(:答：不一样。.222)2(44的底数是，的底数是①底数不同：积的相反数相乘的个表示相乘，个表示②意义不同：24224)2(44的相反数次方的读作次方，的读作③读法不同：42242)2(4416)2222(216)2()2()2()2()2(44④计算结果不同：一样吗？为什么？与思考442)2(:答：不一样。.222)2(44的底数是，的底数是①底数不同：积的相反数相乘的个表示相乘，个表示②意义不同：24224)2(44的相反数次方的读作次方，的读作③读法不同：42242)2(4416)2222(216)2()2()2()2()2(44④计算结果不同：（1）1的任何次幂得1；（2）-1的奇次幂是-1，偶次幂是1。（3）任何数的偶数次幂都是非负数（比较常用的是2次方，如a²≥0）1ⁿ=1，(-1)²ⁿ=1，(-1)2n+1=-1具有特殊性质数的幂重点探究：1.通过思考题讨论究竟底数是谁（幂的符号与底数的符号判断）2.有理数的乘方的运算步骤要求：①独立完成会做的题目，仔细思考不会写的题目。②理清要讨论的问题，能在讨论环节有针对性的讨论。——成长与精彩属于我们百家争鸣，百花齐放练一练1.下列各数中，数值相等的有①32和23②-27和（-2）7③22和（-2）2④和-1⑤和22451625101②③⑤✔✔✘✘22451625101小结1.乘方运算可以转化成乘法运算，遵循乘法法则正数的任何次幂都是正数。0的任何正整数次幂都是0。负数的乘方运算：先判断符号再将绝对值相乘。2.正确判断幂的符号和底数的符号3737依据奇数指数偶数1ⁿ=1，(-1)²ⁿ=1，(-1)2n+1=-13737的区别与联系及nnnaaa)(,.3相同点指数都是n不同点意义不同底数不同联系n为奇数n为偶数n为正整数nanana)(n个a相乘n个a相乘的积的相反数n个-a相乘a-aa-aⁿ=(-a)ⁿ，且-aⁿ，(-a)ⁿ都与aⁿ互为相反数(a≠0)aⁿ=(-a)ⁿ，且aⁿ，(-a)ⁿ都与-aⁿ互为相反数(a≠0)aⁿ=-aⁿ=(-a)ⁿ=0(a=0)的区别与联系及nnnaaa)(,.3nanana)(