第11课时-一元一次不等式(组)

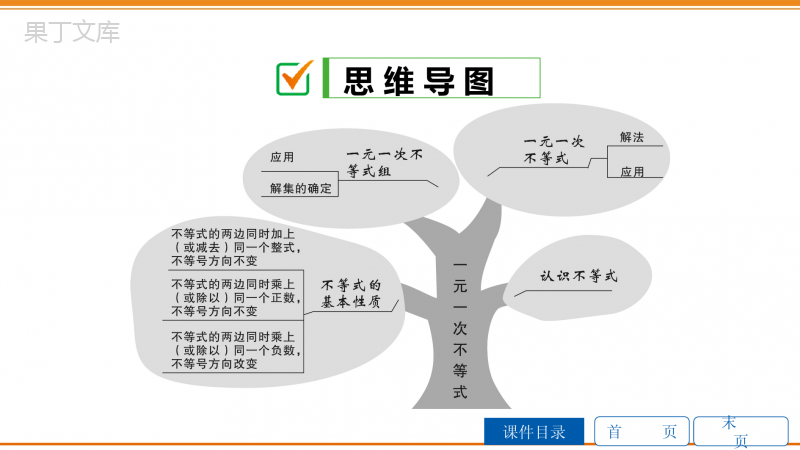
首页课件目录末页第一部分数与代数第四章不等式(组)思维导图考点管理中考再现课时作业归类探究第11课时一元一次不等式(组)首页课件目录末页思维导图首页课件目录末页考点管理1．不等式的概念定义：用不等号(“<”“≤”“>”“≥”或“≠”)表示不等关系的式子叫做不等式．不等式的解：使不等式成立的叫做不等式的解．不等式的解集：一个含有未知数的不等式的所有的解，组成这个不等式的解集．解不等式：求不等式的的过程叫做解不等式．未知数的值解集首页课件目录末页2．不等式的性质性质1：不等式的两边都加(或减)同一个数(或式子)，不等号的方向不变，即如果a>b，那么a±cb±c.性质2：不等式的两边都乘(或除以)同一个正数，不等号的方向不变，即如果a>b，c>0，那么acbcacbc.性质3：不等式的两边都乘(或除以)同一个负数，不等号的方向改变，即如果a>b，c<0，那么acbcacbc.>>><<首页课件目录末页3．一元一次不等式定义：只含有未知数，未知数的次数是的不等式叫做一元一次不等式．求解步骤：一般地，利用，采取与解一元一次方程相类似的步骤，就可以求出一元一次不等式的解集．注意：当不等式的两边都乘(或除以)同一个负数时，不等号的方向要．一个1不等式的性质改变首页课件目录末页4．一元一次不等式组定义：关于同一个未知数的几个一元一次不等式合在一起，就组成一个．解集：一元一次不等式组中各个不等式的解集的，叫做这个一元一次不等式组的解集．一元一次不等式组公共部分首页课件目录末页解集的四种情况：已知a>b.(1)如图，不等式组x>a，x>b的解集为，口诀：同大取大．x>a首页课件目录末页(2)如图，不等式组xb的解集为，口诀：大小小大中间找．(4)如图，不等式组x>a，x－1的解集在数轴上表示为()B首页课件目录末页【解析】本题考查了一元一次不等式组的解集在数轴上的表示，先解这个不等式组的解集为－12(x＋4)的解为.【解析】去括号，得3x＋1>2x＋8，移项，得3x－2x>8－1，整理，得x>7.3．[2019·长沙]不等式组x＋1≥0，3x－6<0的解集是.【解析】先确定不等式组中每个不等式的解集，然后利用口诀寻找两个不等式解集的公共部分．解不等式x＋1≥0，得x≥－1；解不等式3x－6<0，得x<2.根据“大小小大中间找”确定不等式组的解集是－1≤x<2.x>7－1≤x<2首页课件目录末页4．[2019·邵阳]不等式组x＋4<3，1－x3≤1的解集是.【解析】解不等式x＋4<3，得x<－1.解不等式1－x3≤1，得x≥－2.∴不等式组的解集为－2≤x<－1.－2≤x<－1首页课件目录末页5．[2019·益阳]不等式组x－1<0，－x>3的解集为.【解析】x－1<0，①－x>3.②解不等式①，得x<1.解不等式②，得x<－3.∴原不等式组的解集为x<－3.x<－3首页课件目录末页6．[2019·株洲]若a为有理数，且2－a的值大于1，则a的取值范围为.【解析】根据不等式的性质，将2－a>1，变形为－a>－1，不等式两边都除以－1，得a<1.a<1首页课件目录末页归类探究类型之一不等式的概念和性质[2019·广安]若m>n，则下列不等式不一定成立的是()A．m＋3>n＋3B.－3m<－3nC.m3>n3D.m2>n2D首页课件目录末页【解析】不等式的两边都加3，不等号的方向不变，故A不符合题意；不等式的两边都乘－3，不等号的方向改变，故B不符合题意；不等式的两边都除以3，不等号的方向不变，故C不符合题意；如m＝2，n＝－3，m>n，m2－3，并把它的解集在数轴上表示出来．首页课件目录末页解：去分母，得2(x－2)－5(x＋4)>－30，去括号，得2x－4－5x－20>－30，移项、合并同类项，得－3x>－6，系数化为1，得x<2.不等式的解集在数轴上表示如答图．例2答图首页课件目录末页【点悟】解一元一次不等式与解一元一次方程类似，不同的是不等式两边都乘(或除以)同一个负数时，不等号的方向要改变．用数轴表示解集时，要注意实心点与空心圈的区别．首页课件目录末页类型之三解一元一次不等式组[2019·江西]解不等式组2x＋1>x，1－2x≥x＋72，并在数轴上表示它的解集．首页课件目录末页解：2x＋1>x，①1－2x≥x＋72.②解不等式①，得x>－2.解不等式②，得x≤－1.∴不等式组的解集为－21－x2，3x－731－x2，①3x－7313.解不等式②，得x<4.∴不等式组的解集为13b)：(1)若x>a，x>b，则x>a；(2)若xb，则ba，x0，2x＋1>3的解集为x>1，则m的取值范围是.【解析】分别解两个不等式，得x>m，x>1.∵该不等式组的解集是x>1，∴m≤1.m≤1首页课件目录末页2．[2019·聊城]若不等式组x＋132【解析】解不等式①，得x>8，由不等式②，知x<4m，当4m≤8时，原不等式无解，∴m≤2.故选A.A首页课件目录末页3．[2019·宜宾]若关于x的不等式组x－24－2.－2≤m<1首页课件目录末页解不等式②，得x≤m＋23.∴不等式组的解集为－2b且acb且acb，c<0条件，故满足条件的对应点的位置可以是A.选项B不满足a>b，选项C，D不满足c<0，故满足条件的对应点的位置不可以是B，C，D.故选A.首页课件目录末页2．[2019·陇南]不等式2x＋9≥3(x＋2)的解集是()A．x≤3B.x≤－3C．x≥3D.x≥－3【解析】∵2x＋9≥3(x＋2)，∴2x＋9≥3x＋6，∴x≤3.故选A.A首页课件目录末页3．[2019·宿迁]不等式x－1≤2的非负整数解有()A．1个B.2个C．3个D.4个【解析】∵x－1≤2，解得x≤3，∴不等式x－1≤2的非负整数解有0,1,2,3，共4个．故选D.D首页课件目录末页4．[2019·乐山]不等式组2x－6<3x，x＋25－x－14≥0的解集在数轴上表示正确的是()【解析】由第1个不等式解得x>－6，由第2个不等式解得x≤13.故选B.B首页课件目录末页5．[2019·德州]不等式组5x＋2>3x－1，12x－1≤7－32x的所有非负整数解的和是()A．10B.7C．6D.0A首页课件目录末页【解析】解第一个不等式，得x>－52.解第二个不等式，得x≤4.∴不等式组的解集为－523，x－12≤4的解为.【解析】解不等式x＋2>3，得x>1.解不等式x－12≤4，得x≤9.根据“大小小大中间找”确定不等式组的解集是11，①12x－2≤2.②解不等式①，得x>6.解不等式②，得x≤8.∴不等式组的解集为6－6x＋1，x－k>1的解集为x>－1，则k的取值范围是.【解析】解第一个不等式，得x>－1，解第二个不等式，得x>k＋1，根据同大取大的原则，k＋1≤－1，解得k≤－2.k≤－2首页课件目录末页三、解答题(共30分)10．(10分)[2018·桂林]先解不等式5x－130，3x－8≤－x，并把解集在数轴上表示出来．解：不等式①的解集为x>－1.不等式②的解集为x≤2.∴原不等式组的解集为－10有解，则在其解集中，整数的个数不可能是()A．1B.2C．3D.4C首页课件目录末页【解析】由原不等式组得x<6－m2，x>m4，这时原不等式组的解为m451－x有且仅有三个整数解，且使关于y的分式方程1－2yy－1－a1－y＝－3的解为正数，则所有满足条件的整数a的值之和是()A．－3B.－2C．－1D.1A首页课件目录末页【解析】根据解一元一次不等式组的基本步骤解x3－2≤14x－7，①6x－2a>51－x，②解不等式①，得x≤3.解不等式②，得x>5＋2a11.∵不等式组有且仅有3个整数解，∴三个整数解分别为：3,2,1.首页课件目录末页∴0≤5＋2a11<1.解得－2.5≤a<3.解分式方程1－2yy－1－a1－y＝－3，得y＝2－a.根据分式方程的解为正数和分式方程的分母不能为0，得y>0，y≠1，即2－a>02－a≠1.首页课件目录末页解得a<2且a≠1.∴－2.5≤a<2且a≠1，∴满足条件的整数a为－2，－1,0.它们的和为－2－1＋0＝－3.故选A.首页课件目录末页15．(4分)[2019·内江]若关于x的不等式组x2＋x＋13>0，3x＋5a＋4>4x＋1＋3a恰有三个整数解，则a的取值范围是.10，得x>－25.解不等式3x＋5a＋4>4(x＋1)＋3a，得x<2a.∵不等式组恰有三个整数解，∴这三个整数解为0,1,2.∴2<2a≤3，解得1y，则k的取值范围为.解：方法一：2x－3y＝5，①x－2y＝k.②①－②，得x－y＝5－k，∵x>y，∴5－k>0，∴k<5.k<5首页课件目录末页方法二：2x－3y＝5，x－2y＝k.解得x＝－3k＋10，y＝－2k＋5.∵x>y，∴－3k＋10>－2k＋5，∴k<5.首页课件目录末页(12分)17．(12分)[2019·凉山]根据有理数乘法(除法)法则可知：①若ab>0或ab>0，则a>0，b>0或a<0，b<0；②若ab<0或ab<0，则a>0，b<0或a<0，b>0.根据上述知识，求不等式(x－2)(x＋3)>0的解集．首页课件目录末页解：原不等式可化为：①x－2>0，x＋3>0或②x－2<0，x＋3<0.由①，得x>2.由②，得x<－3.∴原不等式的解集为x<－3或x>2.首页课件目录末页请你运用所学知识，结合上述材料解答下列问题：(1)不等式x2－2x－3<0的解集为；(2)求不等式x＋41－x<0的解集(要求写出解答过程)．－10，x＋1<0或②x－3<0，x＋1>0.由①，得不等式组无解．由②，得－10，1－x<0或②x＋4<0，1－x>0.由①，得x>1.由②，得x<－4.∴原不等式的解集为x>1或x<－4.