专题提升(十二)-与圆的切线有关的计算与证明

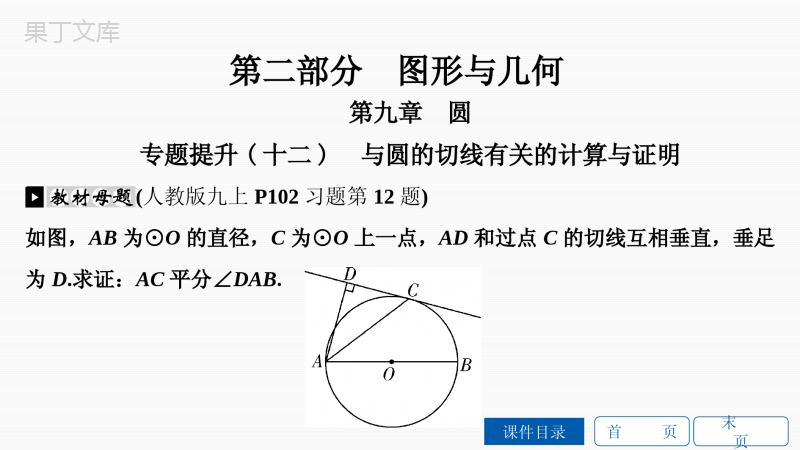
首页课件目录末页第二部分图形与几何第九章圆专题提升(十二)与圆的切线有关的计算与证明(人教版九上P102习题第12题)如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D.求证：AC平分∠DAB.首页课件目录末页证明：如答图，连接OC.∵CD是⊙O的切线，∴OC⊥CD.又AD⊥CD，∴OC∥AD.∴∠1＝∠2.∵OC＝OA，∴∠1＝∠3.∴∠2＝∠3，即AC平分∠DAB.【思想方法】已知圆的切线，可得切线垂直于过切点的半径(若图中未画出，通常需要连半径作辅助线)．首页课件目录末页[2019·天津]已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为⊙O上一点．(1)如图①，求∠ACB的大小；(2)如图②，AE为⊙O的直径，AE与BC相交于点D，若AB＝AD，求∠EAC的大小．首页课件目录末页解：(1)如答图①，连接OA，OB.∵PA，PB分别是切线，∴OA⊥PA，OB⊥PB，即∠PAO＝∠PBO＝90°.∵∠APB＝80°，∴在四边形OAPB中，∠AOB＝360°－90°－90°－80°＝100°，∴∠ACB＝12∠AOB＝50°.中考变形答图①首页课件目录末页(2)如答图②，连接CE.∵AE为直径，∴∠ACE＝90°，由(1)知，∠ACB＝50°，∴∠BCE＝∠ACE－∠ACB＝40°，∴∠BAE＝∠BCE＝40°.中考变形答图②首页课件目录末页∵在△ABD中，AB＝AD，∴∠ADB＝∠ABD＝70°.∵在△ACD中，∠ADB是外角，∴∠EAC＝∠ADB－∠ACB＝70°－50°＝20°.首页课件目录末页如图，已知三角形ABC的边AB是⊙O的切线，切点为B.AC经过圆心O并与圆相交于点D，C，过点C作直线CE⊥AB，交AB的延长线于点E.(1)求证：CB平分∠ACE；(2)若BE＝3，CE＝4，求⊙O的半径．首页课件目录末页(1)证明：如答图，连接OB.∵AB是⊙O的切线，∴OB⊥AB.∵CE⊥AB，∴OB∥CE，∴∠1＝∠3.∵OB＝OC，∴∠1＝∠2，∴∠2＝∠3，∴CB平分∠ACE.首页课件目录末页(2)解：如答图，连接BD.∵CE⊥AB，∴∠E＝90°，∴BC＝BE2＋CE2＝32＋42＝5.∵CD是⊙O的直径，∴∠DBC＝90°，∴∠E＝∠DBC，由(1)知∠2＝∠3，中考预测答图首页课件目录末页∴△DBC∽△BEC，∴CDCB＝BCEC，∴BC2＝CD·CE，∴CD＝524＝254，∴OC＝12CD＝258，∴⊙O的半径为258.首页课件目录末页类型之二与圆的切线的判定有关的计算或证明(人教版九上P101习题第4题)如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB.求证：直线AB是⊙O的切线．首页课件目录末页证明：如答图，连接OC.∵OA＝OB，CA＝CB，∴△OAB是等腰三角形，OC是底边AB上的中线．∴OC⊥AB.∴AB是⊙O的切线．【思想方法】证明圆的切线的两种常用思路：(1)作半径，证垂直；(2)作垂直，证半径．首页课件目录末页1．[2018·青海]如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上一点，且AP＝AC.(1)求证：PA是⊙O的切线；(2)若PD＝5，求⊙O的直径．首页课件目录末页(1)证明：如答图，连接OA.∵∠B＝60°，∴∠AOC＝2∠B＝120°.又∵OA＝OC，∴∠OAC＝∠OCA＝30°.又∵AP＝AC，∴∠P＝∠ACP＝30°.首页课件目录末页∴∠OAP＝∠AOC－∠P＝90°.∴OA⊥PA.∵OA为⊙O的半径，∴PA是⊙O的切线．首页课件目录末页(2)解：在Rt△OAP中，∵∠P＝30°，∴PO＝2OA＝OD＋PD.又∵OA＝OD，∴PD＝OA.∵PD＝5，∴OA＝5.∴⊙O的直径为25.首页课件目录末页2．[2019·雅安]如图，已知AB是⊙O的直径，AC，BC是⊙O的弦，OE∥AC交BC于点E，过点B作⊙O的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F.(1)求证：DC是⊙O的切线；(2)若∠ABC＝30°，AB＝8，求线段CF的长．首页课件目录末页(1)证明：如答图，连接OC.∵OE∥AC，∴∠1＝∠ACB.∵AB是⊙O的直径，∴∠1＝∠ACB＝90°，∴OD⊥BC.由垂径定理，得OD垂直平分BC，∴DB＝DC，∴∠DBE＝∠DCE.又∵OC＝OB，∴∠OBE＝∠OCE，即∠DBO＝∠OCD.首页课件目录末页∵DB为⊙O的切线，OB是半径，∴∠DBO＝90°，∴∠OCD＝∠DBO＝90°，即OC⊥DC.∵OC是⊙O的半径，∴DC是⊙O的切线．首页课件目录末页(2)解：在Rt△ABC中，∠ABC＝30°，∴∠2＝60°.又OA＝OC，∴△AOC是等边三角形，∴∠COF＝60°.在Rt△ABC中，∵AB＝8，∴OC＝12AB＝4.tan∠COF＝CFOC＝3，∴CF＝43.首页课件目录末页3．[2019·菏泽]如图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AB，交BC的延长线于点D，交AC于点E，F是DE的中点，连接CF.(1)求证：CF是⊙O的切线；(2)若∠A＝22.5°，求证：AC＝DC.首页课件目录末页(1)证明：∵AB是⊙O的直径，∴∠ACB＝∠ACD＝90°.∵点F是ED的中点，∴CF＝EF＝DF，∴∠AEO＝∠FEC＝∠FCE.首页课件目录末页∵OA＝OC，∴∠OCA＝∠OAC.∵OD⊥AB，∴∠OAC＋∠AEO＝90°，∴∠OCA＋∠FCE＝90°，即OC⊥FC，∴CF是⊙O的切线．首页课件目录末页(2)解：如答图，连接AD.∵OD⊥AB，AC⊥BD，∴∠AOE＝∠ACD＝90°.∵∠AEO＝∠DEC，∴∠OAE＝∠CDE＝22.5°.∵AO＝BO，OD⊥AB，易证AD＝BD.首页课件目录末页∴∠ADO＝∠BDO＝22.5°，∴∠ADB＝45°，∴∠CAD＝∠ADC＝45°，∴AC＝CD.首页课件目录末页如图，AB是⊙O的直径，D为⊙O上一点，AT平分∠BAD，交⊙O于点T，过点T作TC⊥AD，交AD的延长线于点C.(1)求证：CT为⊙O的切线；(2)若⊙O的半径为2，CT＝3，求AD的长．首页课件目录末页(1)证明：如答图，连接OT.∵OA＝OT，∴∠OAT＝∠OTA.又∵AT平分∠BAD，∴∠DAT＝∠OAT.∴∠DAT＝∠OTA.∴OT∥AC.又∵CT⊥AC，∴CT⊥OT.∴CT为⊙O的切线．首页课件目录末页(2)解：如答图，过点O作OE⊥AD于点E，则点E为AD的中点．又∵CT⊥AC，∴OE∥CT.又∵OT∥AC，∴四边形OTCE为矩形．∵CT＝3，∴OE＝3.∴在Rt△OAE中，AE＝OA2－OE2＝22－32＝1.∴AD＝2AE＝2.