故障树分析 (1),故障树分析法计算方法

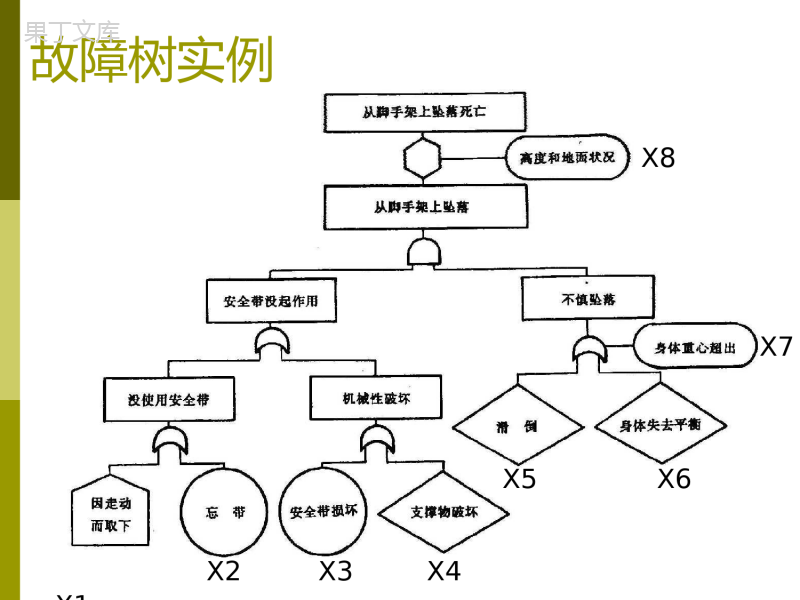
系统安全第六章故障树分析故障树分析的起源美国贝尔实验室H.A.Watson民兵式导弹发射控制系统美国贝尔实验室A.B.Mearns火箭偶发事故预测美国波音飞机公司Hassl电子计算机进行辅助分析和计算美国原子能委员会拉马森报告故障树实例X8X7X5X6X4X2X3故障树与事件树演绎分析法和归纳分析法静态和动态微观和宏观故障树故障树：演绎地表示故障事件发生原因及其逻辑关系的逻辑树图。事件：输入事件，输出事件；顶事件，中间事件，基本事件。逻辑门：逻辑或门，逻辑与门，控制门，条件门。FTA分析中的标准符号顶事件/中间事件基本事件省略符号正常事件转移符号转移符号FTA分析中的标准符号+·逻辑与门逻辑或门控制门条件门条件门故障树结构函数用布尔代数表达故障树事件间的逻辑关系得到的数学表达式。用逻辑积表示逻辑与，记为或·用逻辑和表示逻辑或，记为或＋示例故障树的结构函数87654321)()(XXXXXXXXT顶事件发生概率-基本事件统计独立逻辑积的概率逻辑和的概率示例故障树的概率函数niinnrppppXXXP12121)(niinNrppppXXXP12121)1(1)1()1)(1(1)(87654321)]1)(1(1[)]1)(1)(1)(1(1[)(pppppppppP布尔代数运算法则幂等律A+A=AA·A=A加法交换律A+B=B+A乘法交换律A·B=B·A加法结合律A+(B+C)=(A+B)+C乘法结合律A·(B·C)=(A·B)·C加法分配律A·B+A·C=A·(B+C)乘法分配率(A+B)·(A+C)=A+(B·C)加法吸收律A+(A·B)=A乘法吸收律A·(A+B)=A布尔代数运算法则¤对偶法则¤对合法则¤重叠法则BABABABAAA)(BAABABAABA可靠性框图与FTA－串联模型可靠度:R=R1.R2不可靠度:F=F1+F2-F1F2可靠性框图与FTA－并联模型可靠度R=R1+R2-R1.R2不可靠度F=F1F2故障树的简化为了进行定量计算和处理共因事件，需对已建好的故障树进行简化。化简可依据上级事件发生的必要条件进行，也可用布尔代数运算进行。全为AND门时运算：Z=A·E1=A·B·E2=A·B·C·D全为OR门运算：Z=A＋E1=A＋B＋E2=A＋B＋C＋D有共因事件时的简化（a）Txxxx1213()0019.0)1.01()1.01(11.01.0)1)(1(1)(3121qqqqqgqqq12301.如果（b）21321213211213121)(xxxxxxxxxxxxxxxxxTgqqq()...120101001有共因事件时的简化Z=A+E=A+(A·B)=AZ=A·E=A·(A+B)=A有共因事件时的简化Z=E1+E2=(A·B)+(A·C)=A·(B+C)Z=E1·E2=(A+B)·(A+C)=A+(B·C)最小割集合与最小径集合割集合：能使顶事件发生的基本事件集合。最小割集合：其中任一基本事件不发生则顶事件就不发生的割集合。指明事故发生模式径集合：其中基本事件都不发生则顶事件不发生的基本事件集合。最小径集合：其中任一基本事件不发生对保证顶事件不发生都是必要的径集合。指明预防事故途径最小割集合求法观察法布尔代数法行列法最小割集合求法-观察法X8X7X5X6X4X1X2X3(,,,)xxxx1578(,,,)xxxx2578(,,,)xxxx3578(,,,)xxxx4578(,,,)xxxx1678(,,,)xxxx2678(,,,)xxxx3678(,,,)xxxx4678最小割集合：最小割集合求法-布尔代数法Txxxxx()()12143324221314111xxxxxxxxxxxxxxxxx12423()x1(,)xx23(,)xx24最小割集合为：最小割集合求法-行列法TGGxGxGxxxxxxxxxxxxxxxxx12122211131421232412324,,,,,,,,,,,最小径集合求法观察法对偶故障树法（成功树）最小径集合求法-观察法X8X7X5X6X4X1X2X3),,,(4321xxxx),(65xx()x7()x8最小径集合：最小径集合求法-成功树4312121xxxxxGGT)()(34121xxxxxT最小径集合：(,)xx12(,,)xxx134顶事件发生概率直接计算法最小割集合法不交化法直接计算法当基本事件发生概率很小，逻辑和的概率：当基本事件发生概率很小，逻辑积的概率：niinnqqqqxxxqg12121)Pr()(niinnqqqqxxxqg12121)Pr()(最小割集合法当故障树中，最小割集中无相同的基本事件（各最小割集不相交），或基本事件数量少时，直接计算法是可行的，也是可以理解的。当故障树复杂或最小割集中有相同基本事件且其概率不可忽略时，计算比较复杂且易出错。此时用最小割集进行计算比较合适。在求出最小割集的基础上，把故障树顶事件表示为最小割集中基本事件积之和的布尔表达式。计算的条件是基本事件是相互独立的并且已知其发生的概率。若相当多的基本事件不能估计或给出其概率时，则不宜进行定量分析，只可进行定性分析。最小割集合法最小割集之间相交时:)()()()()(211rjrJjKPKPKPKPKPQ)()()()(121321211rrKKKKPKKKPKKPKPQ最小割集之间完全不相交时:最小割集合法-近似计算S1-是首项近似算式；r-是最小割集数；kj-是第j个最小割集的集合；Xi-第j个最小割集中第i个底事件；n-第j个最小割集中底事件的个数；S2-近似计算的第二项。2121121)(21SSSSSQrjjkpS1)(1niijXk1rjijikkpS12)(计算示例：则：设基本事件X1,X2,X3,X4,X5的概率为q1=q2=q3=q4=q5=0.015,4,3,3,2,3,1,2,1XXXXXXXXX5,4,34,3,23,3,12,2,11XXXkXXkXXkXXk000301.0)543()32()31()21()4()3()2()1()(154323132141qqqqqqqqqXXXPXXPXXPXXPKPKPKPKPKPSJJ设一故障树的最小割集是:0000030201.0......)43()42()32()41()31()21()(5432543132154321321321543325433131235432132213121412＝qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqKKPKKPKKPKKPKKPKKPKKPSjiji00029949.02211SSQ所以：计算示例：不交化法利用布尔代数运算法则使相交的，即相互统计不独立的最小割集合（例如，同一基本事件在不同的最小割集合中出现的情况）变为不交的，即相互统计独立且互斥的最小割集合，然后按各最小割集合发生概率的代数和来计算顶事件发生概率。不交化法1）若集合A和B不包含共同基本事件，则AB可以先按对偶法则将集合A变换后按重叠法则进行不交化，再按分配法则展开。2）若集合A和B包含共同基本事件，则ABAB0A0—除去与集合B共有的基本事件后，A集合中剩余的基本事件的集合。3）若集合A和C包含共同基本事件，集合B和C也包含共同基本事件，则ABCABC00A0—除去与集合C共有的基本事件后，A集合中剩余的基本事件的集合；B0—除去与集合C共有的基本事件后，B集合中剩余的基本事件的集合。4）若集合A和C包含共同基本事件，集合B和C也包含共同基本事件，且AB（A属于B），则ABCBC00不交化法TXXXXX12423XXXXXXX1124123XXXXXXXX11241234q1001.，q2002.，q3003.，q4004.，gqqqqqqqqq()()()()112412341110110102041010203104.(.)..(.)..(.)02044.基本事件重要度从可靠性、安全性角度看，系统中各部件并不是同等重要的，引入重要度的概念用以标明某个部件对顶事件发生的影响大小是很必要的。在故障树分析中，用基本事件重要度来衡量某一基本事件对顶事件影响的大小。重要度是故障树分析中的一个重要概念，对改进系统设计，制订维修策略是十分有利的。对于不同的对象和要求，应采用不同的重要度。在故障树分析中常用的基本事件重要度有结构重要度、概率重要度和临界重要度。基本事件结构重要度基本事件在最小割集合（或最小径集合）中出现的情况直接反映了该基本事件的重要度：在由较少基本事件组成的最小割集合（或最小径集合）中出现的基本事件，其结构重要度较大；在不同最小割集合（或最小径集合）中出现次数多的基本事件，其结构重要度大。结构重要度：mjjRkiI111)(k—故障树包含的最小割集合（或最小径集合）数目；m—包含第i个基本事件的最小割集合（或最小径集合）数目；Rj—包含第i个基本事件的第j个最小割集合（或最小径集合）中基本事件的数目。基本事件结构重要度该故障树的最小割集合为)(1x，),(32xx，),(42xx。则各基本事件的结构重要度：311131)1(I31212131)2(I612131)4()3(II得到：)4()3()2()1(IIII。显然该结果不符合实际情况。该故障树的最小径集合为(,)xx12，(,,)xxx134。则各基本事件的结构重要度：125312121)1(I412121)2(I613121)4()3(II得到：)4()3()2()1(IIII。概率重要度基本事件概率重要度反映基本事件发生概率的变化对顶事件发生概率的影响。概率重要度：igqqgiI)()(gq()—故障树的概率函数；qi—第i个基本事件的发生概率。概率重要度假设各基本事件发生概率分别为q1001.，q2002.，q3003.，q4004.，q5005.，则基本事件x1的概率重要度为)]1)(1(1[)]}1)(1(1[1{1)()1(5352341qqqqqqqqgIg0078.类似地，Ig().2002，Ig().30049，Ig().40031，Ig().5001。则各基本事件概率重要度次序为：)2()5()4()3()1(gggggIIIII假设各基本事件发生概率分别为q1001.，q2002.，q3003.，q4004.，q5005.，则基本事件x1的概率重要度为)]1)(1(1[)]}1)(1(1[1{1)()1(5352341qqqqqqqqgIg0078.类似地，Ig().2002，Ig().30049，Ig().40031，Ig().5001。则各基本事件概率重要度次序为：)2()5()4()3()1(gggggIIIII假设各基本事件发生概率分别为q1001.，q2002.，q3003.，q4004.，q5005.，则基本事件x1的概率重要度为)]1)(1(1[)]}1)(1(1[1{1)()1(5352341qqqqqqqqgIg0078.类似地，Ig().2002，Ig().30049，Ig().40031，Ig().5001。则各基本事件概率重要度次序为：)2()5()4()3()1(gggggIIIII：临界重要度临界重要度为顶事件发生概率的相对变化率与基本事件发生概率的相对变化率之比。临界重要度：)()()(qgqiIiIigc临界重要度各基本事件临界重要度为：Ic().1039，Ic().2002，Ic().3074，Ic().4062，Ic().5025。各基本事件临界重要度次序为：IIIIIccccc()()()()()34152故障树分析故障树分析从特定的故障事件开始，利用故障树研究可能引起该事件发生的各种原因事件及其相互关系的系统安全分析方法。定性分析：编制故障树，找出导致顶事件发生的全部基本事件找出最小割集合、最小径集合；确定各基本事件的重要度。定量分析：计算顶事件发生概率故障树的优点它是一种从系统到部件，再到零件，按“下降形”分析的方法。它对系统故障不但可以做定性的而且还可以做定量的分析；不仅可以分析由单一构件所引起的系统故障，而且也可以分析多个构件不同模式故障而产生的系统故障情况。由于故障树是一种逻辑门所构成的逻辑图，因此适合于用电子计算机来计算；而且对于复杂系统的故障树的构成和分析，也只有在应用计算机的条件下才能实现。故障树的缺点构造故障树的多余量相当繁重，难度也较大，对分析人员的要求也较高，因而限制了它的推广和普及。在构造故障树时要运用逻辑运算，在其未被一般分析人员充分掌握的情况下，很容易发生错误和失察。例如，很有可能把重大影响系统故障的事件漏掉；同时，由于每个分析人员所取的研究范围各有不同，其所得结论的可信性也就有所不同。故障树分析用计算机程序60年代人们就开发了故障树分析用计算机程序，然而受当时计算机技术的限制，其应用受到限制。60年代末出现的故障树分析用程序PREP和KITT是最初的实用程序，在第一次核电站危险性评价中得到应用。70年代以后采用各种算法的程序相继问世，迄今各种故障树分析用计算机程序已经多不胜数。按其基本功能，把故障树分析用计算机程序划分为定性分析、定量分析两类。故障树的编制找出可能导致顶事件发生的全部基本事件，弄清基本事件之间、基本事件与顶事件之间的关系。编制故障树的过程是辨识危险源的过程，正确地编制故障树才能正确地辨识危险源。正确地编制故障树是进行后面的定性分析和定量分析的基础。故障树的编制确定顶事件顶事件是被故障树分析的对象，在危险源辨识、控制和评价时，把被分析的系统故障或事故确定为顶事件。为了更有效地进行故障树分析，作为顶事件的系统故障或事故应该能清晰地回答“何时”、“何地”、“何种故障或事故”。故障树的编制规定分析的边界条件硬件系统的边界。包括故障树分析涉及的设备，这些设备与衔接工艺间的交接面，公用供应系统等。分析的深度。分析的详细程度，即查找的基本原因详细到什么程度。初始条件。初始条件包括初始设备条件和初始运转条件。不考虑的事件。有些事件或条件在故障树分析中可以不考虑。现有条件。现有条件是一些在故障树分析中一定要出现的事件或条件。其它前提条件。分析者在进行故障树分析时对系统做的一些有关的假设。故障树的编制在编制过程中应该遵从如下的规则：故障事件的描述。把故障事件写入事件符号中，准确地描述元素及其故障模式。故障事件的分类。在编制故障树时把故障事件划分为两类：元素故障和系统故障。如果是元素故障，则可以在逻辑或门下分别找出元素的原生故障、次生故障和指令故障。完成每个逻辑门。应该完成每个逻辑门的全部输入事件后再去分析其它逻辑门的输入事件。故障树分析实例化学反应失控事故原因分析故障树化学反应装置安全监控系统1）利用温度传感器TE/TT-714监测反应器温度；2）反应器温度升高到107℃时发出声音警报（利用喇叭）；3）反应器温度升高到107℃时关闭电磁阀SV-1，切断物料供给，使反应停止；4）操作者听到报警后可以按下应急按钮关闭电磁阀，切断物料供应，使反应停止。化学反应失控事故原因分析故障树化学反应失控事故原因分析故障树化学反应失控事故原因分析故障树利用计算机程序MOCUS求得故障树的全部最小径集合为(,,,,)CECCE358104(,,,,,,,,)CCCCCEEEE345671235(,,,,,,,,)CEECECCCC3358411121314利用计算机程序PATHCUT由最小径集合求得41个最小割集合：一阶最小割集合2个()C3()E5二阶最小割集合15个(,)EE34(,)EC38(,)EC310(,)EE24(,)EC28(,)EE14(,)EC18(,)EC47(,)CC78(,)EC46(,)CC68(,)EC45(,)CC58(,)EC44(,)CC48三阶最小割集合24个(,,)CCC41011(,,)CCC41012(,,)CCC41013(,,)CCC41014(,,)CCC51011(,,)CCC51012(,,)CCC51013(,,)CCC51014(,,)CCC61011(,,)CCC61012(,,)CCC61013(,,)CCC61014(,,)CCC71011(,,)CCC71012(,,)CCC71013(,,)CCC71014(,,)CCE10111(,,)CCE10121(,,)CCE10131(,,)CCE10141(,,)CCE10112(,,)CCE10122(,,)CCE10132(,,)CCE10142该故障树包含的最小割集合数目较多，且有两个一阶最小割集合，也说明该系统安全性较差。给定基本事件中物的故障率、修理时间和人失误概率等原始数据后，利用计算机程序算出一年中（8760小时）反应失控次数期望值为0.63。化学反应失控事故原因分析故障树系统改进该系统的反应失控故障树中有两个一阶最小割集合（主控制阀故障）和（旁通阀开启），这是一种潜在的严重问题，应该采取措施避免其发生。为此改进系统设计，在主控制阀FICV-702之前增设阀门XV-714，并由电磁阀SV-1控制它。这样，当反应器内温度达到107℃时自动地或人工地利用SV-1切断物料供应。改进后的故障树已经没有一阶最小割集合。假设各基本事件初始数据不变，则改进后系统发生反应失控事故的次数降为0.02次，系统的安全性提高了很多。化学反应失控事故原因分析故障树系统改进系统改进情况故障树修改部分