《正弦函数余弦函数的图象》高一年级下册PPT课件.pptx

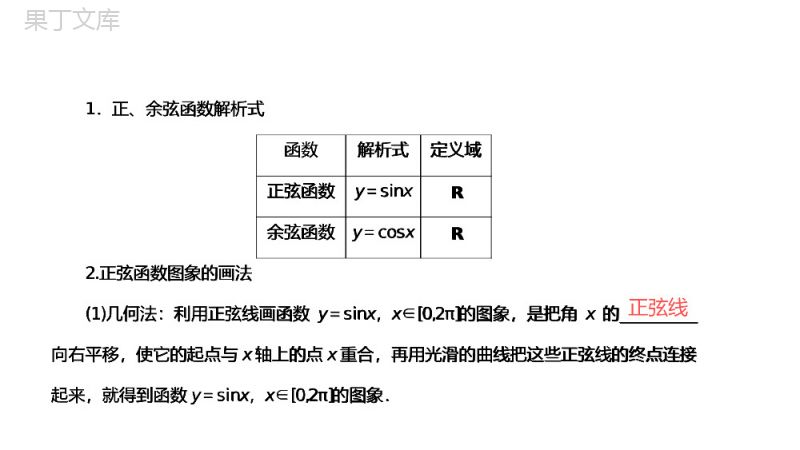
1.4.1正弦函数、余弦函数的图象必修④·人教A版1.4三角函数的图象与性质CONTENTS自主预习学案互动探究学案课时作业学案010203栏目导航自主预习学案第一章三角函数01平静的水面投下一颗石子，荡起阵阵水波．在空间中光波、声波、电磁波无处不在，你可知道，这些波传播的波动图与我们所学的三角函数的图象有着密切的关系吗？正弦线1．正、余弦函数解析式函数解析式定义域正弦函数y＝sinxR余弦函数y＝cosxR2.正弦函数图象的画法(1)几何法：利用正弦线画函数y＝sinx，x∈[0,2π]的图象，是把角x的__________向右平移，使它的起点与x轴上的点x重合，再用光滑的曲线把这些正弦线的终点连接起来，就得到函数y＝sinx，x∈[0,2π]的图象．1．正、余弦函数解析式函数解析式定义域正弦函数y＝sinxR余弦函数y＝cosxR2.正弦函数图象的画法(1)几何法：利用正弦线画函数y＝sinx，x∈[0,2π]的图象，是把角x的__________向右平移，使它的起点与x轴上的点x重合，再用光滑的曲线把这些正弦线的终点连接起来，就得到函数y＝sinx，x∈[0,2π]的图象．第一章三角函数(2)五点法：用“五点法”作函数y＝sinx，x∈[0,2π]的图象的步骤是：①列表：x0π2π3π22πy＝sinx010－10②描点：在平面直角坐标系中描出五点：(0,0)，______________，(π，0)，(3π2，－1)，(2π，0)．③用______________顺次连接这五个点，得正弦曲线在[0,2π]上的简图．y＝sinx，x∈[0,2π]的图象向______、______平行移动(每次2π个单位长度)，就可以得到正弦函数y＝sinx，x∈R的图象．光滑的曲线(π2，1)左右(2)五点法：用“五点法”作函数y＝sinx，x∈[0,2π]的图象的步骤是：①列表：x0π2π3π22πy＝sinx010－10②描点：在平面直角坐标系中描出五点：(0,0)，______________，(π，0)，(3π2，－1)，(2π，0)．③用______________顺次连接这五个点，得正弦曲线在[0,2π]上的简图．y＝sinx，x∈[0,2π]的图象向______、______平行移动(每次2π个单位长度)，就可以得到正弦函数y＝sinx，x∈R的图象．(π2，1)第一章三角函数3．正弦曲线、余弦曲线(1)定义：正弦函数y＝sinx，x∈R和余弦函数y＝cosx，x∈R的图象分别叫做________曲线和________曲线．(2)图象：如图所示．正弦余弦第一章三角函数[知识点拨]1.函数y＝sinx，x∈[0,2π]与y＝sinx，x∈R的图象的关系(1)函数y＝sinx，x∈[0,2π]的图象是函数y＝sinx，x∈R的图象的一部分．(2)因为终边相同的角有相同的三角函数值，所以函数y＝sinx，x∈[2kπ，2(k＋1)π]，k∈Z且k≠0的图象与函数y＝sinx，x∈[0,2π]的图象形状完全一致，因此将y＝sinx，x∈[0,2π]的图象向左、右平行移动(每次移动2π个单位长度)，就可得到函数y＝sinx，x∈R的图象．第一章三角函数2．正弦曲线和余弦曲线的关系×1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)作正弦函数和余弦函数的图象时，所取的“五点”是相同的．()(2)正弦曲线和余弦曲线都介于直线y＝1和y＝－1之间．()(3)正弦曲线与余弦曲线都关于原点对称．()(4)将正弦曲线向右平移3π2个单位可得到余弦曲线．()(5)利用正弦线可以作出三角函数的图象．()√×√√1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)作正弦函数和余弦函数的图象时，所取的“五点”是相同的．()(2)正弦曲线和余弦曲线都介于直线y＝1和y＝－1之间．()(3)正弦曲线与余弦曲线都关于原点对称．()(4)将正弦曲线向右平移3π2个单位可得到余弦曲线．()(5)利用正弦线可以作出三角函数的图象．()第一章三角函数2．用五点法画y＝sinx，x∈[0,2π]的图象时，下列哪个点不是关键点()A．(π6，12)B．(π2，1)C．(π，0)D．(2π，0)3．已知正弦函数过点(π6，m)，则m的值为()A．12B．－12C．32D．1AA2．用五点法画y＝sinx，x∈[0,2π]的图象时，下列哪个点不是关键点()A．(π6，12)B．(π2，1)C．(π，0)D．(2π，0)3．已知正弦函数过点(π6，m)，则m的值为()A．12B．－12C．32D．1第一章三角函数4．在“五点法”中，正弦曲线最低点的横坐标与最高点的横坐标的差等于()A．π2B．πC．3π2D．2πB4．在“五点法”中，正弦曲线最低点的横坐标与最高点的横坐标的差等于()A．π2B．πC．3π2D．2π互动探究学案第一章三角函数02用“五点法”作出下列函数的简图：(1)y＝sinx－1，x∈[0,2π]；(2)y＝2＋cosx，x∈[0,2π]．[思路分析]先在[0,2π]上找出五个关键点，再用光滑曲线连接即可．命题方向1用“五点法”作三角函数的图象⇨典例1第一章三角函数[解析](1)列表x0π2π32π2πsinx010－10sinx－1－10－1－2－1描点，连线，如图[解析](1)列表x0π2π32π2πsinx010－10sinx－1－10－1－2－1描点，连线，如图第一章三角函数(2)列表：x0π2π32π2πcosx10－1012＋cosx32123描点连线，如图(2)列表：x0π2π32π2πcosx10－1012＋cosx32123描点连线，如图第一章三角函数『规律总结』用“五点法”画函数y＝Asinx＋b(A≠0)或y＝Acosx＋b(A≠0)在[0,2π]上的简图的步骤：(1)列表：x0π2π32π2πsinx或cosx0或11或00或－1－1或00或1yy1y2y3y4y5(2)描点：在平面直角坐标系中描出下列五个点：(0，y1)，(π2，y2)，(π，y3)，(3π2，y4)，(2π，y5)．(3)连线：用光滑的曲线将描出的五个点连接起来．x0π2π32π2πsinx或cosx0或11或00或－1－1或00或1yy1y2y3y4y5(2)描点：在平面直角坐标系中描出下列五个点：(0，y1)，(π2，y2)，(π，y3)，(3π2，y4)，(2π，y5)．(3)连线：用光滑的曲线将描出的五个点连接起来．第一章三角函数〔跟踪练习1〕用“五点法”画出下列函数在区间[0,2π]上的简图．(1)y＝2－sinx；(2)y＝cosx－1.[解析](1)按五个关键点列表：x0π2π3π22πsinx010－102－sinx21232[解析](1)按五个关键点列表：x0π2π3π22πsinx010－102－sinx21232第一章三角函数描点并将它们用光滑的曲线连接起来(如图(1))．第一章三角函数(2)按五个关键点列表：x0π2π3π22πcosx10－101cosx－10－1－2－10描点并将它们用光滑的曲线连接起来(如图(2))(2)按五个关键点列表：x0π2π3π22πcosx10－101cosx－10－1－2－10描点并将它们用光滑的曲线连接起来(如图(2))第一章三角函数利用图象变换作出下列函数的简图：(1)y＝1－cosx，x∈[0,2π]；(2)y＝sinx，x∈[0,4π]．[思路分析]先作出y＝cosx和y＝sinx，x∈[0,2π]上的图象，再作对称和平移变换．命题方向2利用图象变换作三角函数的图象⇨典例2第一章三角函数[解析](1)首先用五点法作出函数y＝cosx，x∈[0,2π]的图象，再作出y＝cosx关于x轴对称的图象，最后将图象向上平移1个单位．如图(1)所示．第一章三角函数(2)首先用五点法作出函数y＝sinx，x∈[0,4π]的图象，再将x轴下方的部分对称到x轴的上方．如图(2)所示．第一章三角函数『规律总结』1.平移变换(1)函数y＝f(x＋a)的图象是由函数y＝f(x)的图象向左(a>0)或向右(a<0)平移a个单位得到的．(2)函数y＝f(x)＋b的图象是由函数y＝f(x)的图象向上(b>0)或向下(b<0)平移b个单位得到的．2．对称变换(1)函数y＝f(x)的图象是将函数y＝f(x)的图象在x轴上方的部分不动，下方的部分对称翻折到x轴上方得到．第一章三角函数(2)函数y＝f(x)的图象是将函数y＝f(x)的图象在y轴右边的部分不动，并将其对称翻折到y轴左边得到．(3)函数y＝－f(x)的图象与函数y＝f(x)的图象关于x轴对称．(4)函数y＝f(－x)的图象与函数y＝f(x)的图象关于y轴对称．(5)函数y＝－f(－x)的图象与函数y＝f(x)的图象关于原点对称．第一章三角函数〔跟踪练习2〕函数y＝cosxtanx(0≤x≤3π2，且x≠π2)的图象是()D〔跟踪练习2〕函数y＝cosxtanx(0≤x≤3π2，且x≠π2)的图象是()第一章三角函数[解析]将函数写成分段函数可得y＝sinx，0≤x<π2－sinx，π212的解集．画出正弦函数y＝sinx(x∈R)的简图，并根据图象写出y≥12时x的集合．[思路分析](1)作出y＝sinx，与y＝12的图象．(2)确定sinx＝12的x值．(3)确定sinx>12的解集．第一章三角函数[解析]用“五点法”作出y＝sinx的简图．过(0，12)点作x轴的平行线，从图象可看出它在[0,2π]区间与正弦曲线交于(π6，12)，(5π6，12)点，在[0,2π]区间内，y≥12时x的集合为{xπ6≤x≤5π6}，当x∈R时，若y≥12，则x的集合为{xπ6＋2kπ≤x≤5π6＋2kπ，k∈Z}．[解析]用“五点法”作出y＝sinx的简图．过(0，12)点作x轴的平行线，从图象可看出它在[0,2π]区间与正弦曲线交于(π6，12)，(5π6，12)点，在[0,2π]区间内，y≥12时x的集合为{xπ6≤x≤5π6}，当x∈R时，若y≥12，则x的集合为{xπ6＋2kπ≤x≤5π6＋2kπ，k∈Z}．第一章三角函数『规律总结』1.用三角函数的图象解sinx>a(或cosx>a)的方法(1)作出直线y＝a，作出y＝sinx(或y＝cosx)的图象．(2)确定sinx＝a(或cosx＝a)的x值．(3)确定sinx>a(或cosx>a)的解集．2．利用三角函数线解sinx>a(或cosx>a)的方法(1)找出使sinx＝a(或cosx＝a)的两个x值的终边所在的位置．(2)根据变化趋势，确定不等式的解集．第一章三角函数〔跟踪练习3〕不等式cosx>0，x∈[0,2π]的解集是_________________.[解析]由余弦函数图象知，x∈[0，π2)∪(32π，2π]．[0，π2)∪(32π，2π][解析]由余弦函数图象知，x∈[0，π2)∪(32π，2π]．[0，π2)∪(32π，2π]方程sinx＝lgx的实根个数有()A．1个B．2个C．3个D．无穷多个[错解]A，如图所示，y＝sinx与y＝lgx的图象，有且只有1个公共点，故选A．利用正弦函数、余弦函数图象判断方程根的个数典例4第一章三角函数[错因分析]作y＝lgx图象时，没有找准临界点的坐标，只作出了草图．[思路分析]画出y＝sinx的图象后要充分利用y＝lgx过(1,0)点和(10,1)点来确定解的个数，准确画图是解答此类题的关键．[正解]C在同一直角坐标系中作函数y＝sinx与y＝lgx的图象．由图中可以看出两函数图象有三个交点(xi，yi)，其中xi∈(1,10)(i＝1,2,3)是方程sinx＝lgx的解．[误区警示]有些方程从正面直接求解较难时，可通过对方程变形，转化成两个熟悉的函数，再通过画函数图象，利用数形结合求解．第一章三角函数D〔跟踪练习4〕函数y＝sinx与y＝12x的图象在(－π2，π2)上的交点有()A．4个B．3个C．2个D．1个〔跟踪练习4〕函数y＝sinx与y＝12x的图象在(－π2，π2)上的交点有()A．4个B．3个C．2个D．1个1．用“五点法”作出函数y＝3－cosx的图象，下列点中不属于五点作图中的五个关键点的是()A．(π，－1)B．(0,2)C．(π2，3)D．(32π，3)A1．用“五点法”作出函数y＝3－cosx的图象，下列点中不属于五点作图中的五个关键点的是()A．(π，－1)B．(0,2)C．(π2，3)D．(32π，3)第一章三角函数2．函数y＝－sinx，x∈[－π2，3π2]的简图是()D2．函数y＝－sinx，x∈[－π2，3π2]的简图是()第一章三角函数[解析]用特殊点来验证．x＝0时，y＝－sin0＝0，排除选项A、C；又x＝－π2时，y＝－sin(－π2)＝1，排除选项B．[解析]用特殊点来验证．x＝0时，y＝－sin0＝0，排除选项A、C；又x＝－π2时，y＝－sin(－π2)＝1，排除选项B．第一章三角函数3．(2019·广州海珠区期中)函数y＝sinx的定义域为()A．[0，π]B．{第一或第二象限的角}C．{x2kπ≤x≤(2k＋1)π，k∈Z}D．(0，π)[解析]要使函数y＝sinx有意义，则需sinx≥0，由y＝sinx的图象可得{x2kπ≤x≤(2k＋1)π，k∈Z}．C3．(2019·广州海珠区期中)函数y＝sinx的定义域为()A．[0，π]B．{第一或第二象限的角}C．{x2kπ≤x≤(2k＋1)π，k∈Z}D．(0，π)[解析]要使函数y＝sinx有意义，则需sinx≥0，由y＝sinx的图象可得{x2kπ≤x≤(2k＋1)π，k∈Z}．第一章三角函数4．函数y＝sinx，x∈[0,2π]的图象与直线y＝－12的交点有()A．1个B．2个C．3个D．4个B[解析]如图所示，y＝sinx，x∈[0,2π]与y＝－12的图象有2个交点．4．函数y＝sinx，x∈[0,2π]的图象与直线y＝－12的交点有()A．1个B．2个C．3个D．4个[解析]如图所示，y＝sinx，x∈[0,2π]与y＝－12的图象有2个交点．第一章三角函数5．用“五点法”作出下列函数的简图：(1)y＝－sinx(0≤x≤2π)；(2)y＝1＋cosx(0≤x≤2π)．[解析]利用“五点法”作图．(1)列表：x0π2π3π22πsinx010－10－sinx0－1010[解析]利用“五点法”作图．(1)列表：x0π2π3π22πsinx010－10－sinx0－1010第一章三角函数描点作图，如图.描点作图，如图.第一章三角函数(2)列表：x0π2π3π22πcosx10－1011＋cosx21012描点作图，如图．(2)列表：x0π2π3π22πcosx10－1011＋cosx21012描点作图，如图．感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明课时作业学案第一章三角函数03谢谢观看必修④·人教A版新课标导学