《三角函数的诱导公式》高一年级下册PPT课件（第2课时）.pptx

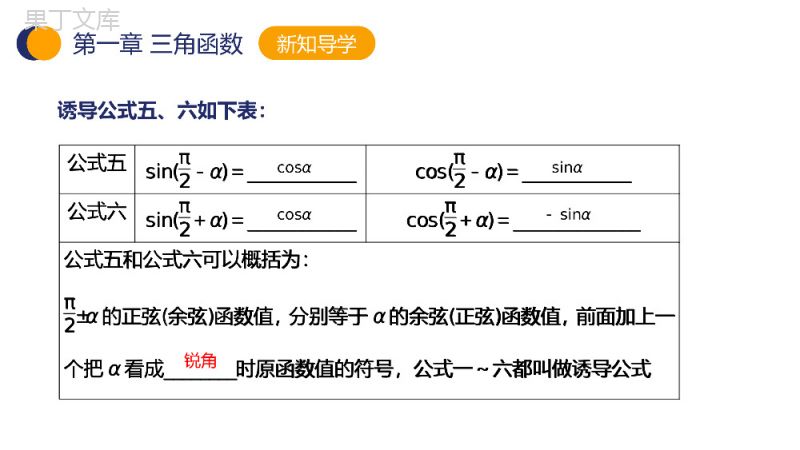
第2课时诱导公式五、六必修④·人教A版1.3三角函数的诱导公式栏目导航自主预习学案互动探究学案课时作业学案010203CONTENTS栏目导航自主预习学案互动探究学案课时作业学案010203CONTENTS自主预习学案01第一章三角函数第一章三角函数情景引入留恋于湖光山色，观山赏水，看山在水中倒映，山的巍峨、水的柔媚在那一刻融合……如果你的手中拿着一个度数为α的角的模型，你观察一下湖中的这个角的模型与你手中的这个角的模型有什么关系？你当然会准确地回答出来：对称！角α关于水平面对称的角的度数是多少？这两个角的三角函数值有什么关系呢？第一章三角函数新知导学诱导公式五、六如下表：cosα公式五sin(π2－α)＝____________cos(π2－α)＝____________公式六sin(π2＋α)＝____________cos(π2＋α)＝______________公式五和公式六可以概括为：π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成________时原函数值的符号，公式一～六都叫做诱导公式sinαcosα－sinα锐角公式五sin(π2－α)＝____________cos(π2－α)＝____________公式六sin(π2＋α)＝____________cos(π2＋α)＝______________公式五和公式六可以概括为：π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成________时原函数值的符号，公式一～六都叫做诱导公式第一章三角函数[知识点拨]1.对诱导公式五、六的两点说明(1)诱导公式五、六反映的是角π2±α与α的三角函数值之间的关系．可借用口诀“函数名改变，符号看象限”来记忆．(2)诱导公式是三角变换的基本公式，其中角可以是一个单角，也可以是一个复角，应用时要注意整体把握，灵活变通．2．对诱导公式一～六的两点说明(1)诱导公式一～六揭示了终边具有某种对称关系的两个角的三角函数之间的关系．[知识点拨]1.对诱导公式五、六的两点说明(1)诱导公式五、六反映的是角π2±α与α的三角函数值之间的关系．可借用口诀“函数名改变，符号看象限”来记忆．(2)诱导公式是三角变换的基本公式，其中角可以是一个单角，也可以是一个复角，应用时要注意整体把握，灵活变通．2．对诱导公式一～六的两点说明(1)诱导公式一～六揭示了终边具有某种对称关系的两个角的三角函数之间的关系．第一章三角函数(2)公式一～六的记忆口诀和说明①口诀：奇变偶不变，符号看象限．②说明：第一章三角函数预习自测×1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)角α的正弦值等于其余角的余弦值．()(2)cos(3π2－α)＝－sinα.()(3)当α是第二象限角时，cos(π2－α)＝－sinα.()(4)sin95°＋cos175°＝0.()(5)已知sin40°＝a，则cos130°＝a.()√×√×1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)角α的正弦值等于其余角的余弦值．()(2)cos(3π2－α)＝－sinα.()(3)当α是第二象限角时，cos(π2－α)＝－sinα.()(4)sin95°＋cos175°＝0.()(5)已知sin40°＝a，则cos130°＝a.()第一章三角函数2．已知sinα＝35，则sin(π2＋α)的值为()A．－35B．－45C．45D．±453．计算：sin211°＋sin279°＝______.4．若cos(π2＋α)＝m，则sinα＝________.D1－m2．已知sinα＝35，则sin(π2＋α)的值为()A．－35B．－45C．45D．±453．计算：sin211°＋sin279°＝______.4．若cos(π2＋α)＝m，则sinα＝________.栏目导航自主预习学案互动探究学案课时作业学案010203CONTENTS互动探究学案02第一章三角函数第一章三角函数互动探究解疑命题方向1利用诱导公式进行化简、求值⇨典例1计算：(1)sin2120°＋cos180°＋tan45°－cos2(－330°)＋sin(－210°)；(2)1＋cos100°sin170°cos370°＋1－sin2170°；[思路分析]利用诱导公式，先化简再求值．计算：(1)sin2120°＋cos180°＋tan45°－cos2(－330°)＋sin(－210°)；(2)1＋cos100°sin170°cos370°＋1－sin2170°；[思路分析]利用诱导公式，先化简再求值．第一章三角函数[解析](1)原式＝sin260°－cos0°＋tan45°－cos230°＋sin30°＝34－1＋1－34＋12＝12.(2)原式＝1＋cos180°－80°sin90°＋80°cos360°＋10°＋1－sin2180°－10°＝1＋－cos80°cos80°cos10°＋1－sin210°＝1－cos280°2cos10°＝sin80°2cos10°＝cos10°2cos10°＝12.[解析](1)原式＝sin260°－cos0°＋tan45°－cos230°＋sin30°＝34－1＋1－34＋12＝12.(2)原式＝1＋cos180°－80°sin90°＋80°cos360°＋10°＋1－sin2180°－10°＝1＋－cos80°cos80°cos10°＋1－sin210°＝1－cos280°2cos10°＝sin80°2cos10°＝cos10°2cos10°＝12.第一章三角函数『规律总结』利用诱导公式化简三角函数式的步骤用诱导公式可把任意角的三角函数转化为锐角三角函数，即口诀是：“负化正，大化小，化到锐角再查表”．第一章三角函数〔跟踪练习1〕sin－α－3π2·sin3π2－α·tan22π－αcosπ2－α·cosπ2＋α·cos2π－α.[解析]原式＝sin－α＋π2·[－sinπ2＋α]·tan22π－αcosπ2－α·cosπ2＋α·cos2π－α＝cosα·－cosα·tan2αsinα·－sinα·cos2α＝tan2αsin2α＝1cos2α.〔跟踪练习1〕sin－α－3π2·sin3π2－α·tan22π－αcosπ2－α·cosπ2＋α·cos2π－α.[解析]原式＝sin－α＋π2·[－sinπ2＋α]·tan22π－αcosπ2－α·cosπ2＋α·cos2π－α＝cosα·－cosα·tan2αsinα·－sinα·cos2α＝tan2αsin2α＝1cos2α.第一章三角函数求证：2sinθ－32πcosθ＋π2－11－2sin2π＋θ＝tan9π＋θ＋1tanπ＋θ－1.命题方向2三角恒等式的证明⇨典例2[思路分析]求证：2sinθ－32πcosθ＋π2－11－2sin2π＋θ＝tan9π＋θ＋1tanπ＋θ－1.[思路分析]第一章三角函数[证明]左边＝－2sin32π－θ·－sinθ－11－2sin2θ＝2sin[π＋π2－θ]sinθ－11－2sin2θ＝－2sinπ2－θsinθ－11－2sin2θ＝－2cosθsinθ－1cos2θ＋sin2θ－2sin2θ＝sinθ＋cosθ2sin2θ－cos2θ＝sinθ＋cosθsinθ－cosθ.右边＝tan9π＋θ＋1tanπ＋θ－1＝tanθ＋1tanθ－1＝sinθ＋cosθsinθ－cosθ.∴左边＝右边，故原式得证．[证明]左边＝－2sin32π－θ·－sinθ－11－2sin2θ＝2sin[π＋π2－θ]sinθ－11－2sin2θ＝－2sinπ2－θsinθ－11－2sin2θ＝－2cosθsinθ－1cos2θ＋sin2θ－2sin2θ＝sinθ＋cosθ2sin2θ－cos2θ＝sinθ＋cosθsinθ－cosθ.右边＝tan9π＋θ＋1tanπ＋θ－1＝tanθ＋1tanθ－1＝sinθ＋cosθsinθ－cosθ.∴左边＝右边，故原式得证．第一章三角函数『规律总结』对于恒等式的证明，应遵循化繁为简的原则，从左边推到右边或从右边推到左边，也可以用左右归一、变更论证的方法．常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法，要熟练掌握基本公式，善于从中选择巧妙简捷的方法．第一章三角函数〔跟踪练习2〕求证：sinθ－5πcosπ2－θsinπ2＋θcos3π－θcos3π2＋θsin－4π－θ＝－1.[证明]左边＝－sin5π－θsinθcosθcosπ－θsinθ[－sin4π＋θ]＝－sinπ－θsinθcosθ－cosθsinθ－sinθ＝－sinθsinθ＝－1＝右边，故原式得证．〔跟踪练习2〕求证：sinθ－5πcosπ2－θsinπ2＋θcos3π－θcos3π2＋θsin－4π－θ＝－1.[证明]左边＝－sin5π－θsinθcosθcosπ－θsinθ[－sin4π＋θ]＝－sinπ－θsinθcosθ－cosθsinθ－sinθ＝－sinθsinθ＝－1＝右边，故原式得证．第一章三角函数学科核心素养化简：sin(4n－14π－α)＋cos(4n＋14π－α)(n∈Z)．分类讨论思想在三角函数化简中的应用典例3[思路分析](1)角中含有变量n，因而需对n的奇偶分类讨论；(2)利用诱导公式，需将角写成符合公式的某种形式，这就需要将角中的某一部分作为一个整体来看．化简：sin(4n－14π－α)＋cos(4n＋14π－α)(n∈Z)．[思路分析](1)角中含有变量n，因而需对n的奇偶分类讨论；(2)利用诱导公式，需将角写成符合公式的某种形式，这就需要将角中的某一部分作为一个整体来看．第一章三角函数[解析]当n为偶数时，设n＝2k(k∈Z)，则原式＝sin(8k－14π－α)＋cos(8k＋14π－α)＝sin[2kπ＋(－π4－α)]＋cos[2kπ＋(π4－α)]＝sin(－π4－α)＋cos(π4－α)＝－sin(π4＋α)＋cos[π2－(π4＋α)]＝－sin(π4＋α)＋sin(π4＋α)＝0.[解析]当n为偶数时，设n＝2k(k∈Z)，则原式＝sin(8k－14π－α)＋cos(8k＋14π－α)＝sin[2kπ＋(－π4－α)]＋cos[2kπ＋(π4－α)]＝sin(－π4－α)＋cos(π4－α)＝－sin(π4＋α)＋cos[π2－(π4＋α)]＝－sin(π4＋α)＋sin(π4＋α)＝0.第一章三角函数当n为奇数时，设n＝2k＋1(k∈Z)，则原式＝sin(8k＋34π－α)＋cos(8k＋54π－α)＝sin[2kπ＋(3π4－α)]＋cos[2kπ＋(5π4－α)]＝sin(3π4－α)＋cos(5π4－α)＝sin[π－(π4＋α)]＋cos[π＋(π4－α)]＝sin(π4＋α)－cos(π4－α)当n为奇数时，设n＝2k＋1(k∈Z)，则原式＝sin(8k＋34π－α)＋cos(8k＋54π－α)＝sin[2kπ＋(3π4－α)]＋cos[2kπ＋(5π4－α)]＝sin(3π4－α)＋cos(5π4－α)＝sin[π－(π4＋α)]＋cos[π＋(π4－α)]＝sin(π4＋α)－cos(π4－α)第一章三角函数『规律总结』1.本题的化简过程，突出体现了分类讨论的思想，当然除了运用分类讨论的思想将n分两类情况来讨论外，在解答过程中还处处体现了化归思想和整体思想．2．在转化过程中，缺乏整体意识，是出错的主要原因．＝sin(π4＋α)－cos[π2－(π4＋α)]＝sin(π4＋α)－sin(π4＋α)＝0.故sin(4n－14π－α)＋cos(4n＋14π－α)＝0.＝sin(π4＋α)－cos[π2－(π4＋α)]＝sin(π4＋α)－sin(π4＋α)＝0.故sin(4n－14π－α)＋cos(4n＋14π－α)＝0.第一章三角函数〔跟踪练习3〕已知A＝sinkπ＋αcosπ2－α＋coskπ－αsinπ2＋α(k∈Z)，则A的值构成的集合是()A．{1，－1,2，－2}B．{－2,0}C．{2，－2}D．{1，－1,0,2，－2}C〔跟踪练习3〕已知A＝sinkπ＋αcosπ2－α＋coskπ－αsinπ2＋α(k∈Z)，则A的值构成的集合是()A．{1，－1,2，－2}B．{－2,0}C．{2，－2}D．{1，－1,0,2，－2}第一章三角函数易错易混警示已知sin(π4－α)＝a,0<α<π2，求sin(5π4＋α)．诱导公式的应用典例4[错解]∵0<α<π2，∴－π4<π4－α<π4，∴cos(π4－α)>0，∴cos(π4－α)＝1－sin2π4－α＝1－a2，sin(5π4＋α)＝sin[3π2－(π4－α)]＝cos(π4－α)＝1－a2.已知sin(π4－α)＝a,0<α<π2，求sin(5π4＋α)．[错解]∵0<α<π2，∴－π4<π4－α<π4，∴cos(π4－α)>0，∴cos(π4－α)＝1－sin2π4－α＝1－a2，sin(5π4＋α)＝sin[3π2－(π4－α)]＝cos(π4－α)＝1－a2.第一章三角函数[错因分析]对诱导公式三角函数值的符号确定掌握不好，在sin[3π2－(π4－α)]中，要把“π4－α”看成锐角来确定三角函数值符号．[思路分析]诱导公式共有六组公式，公式较多，易错记错用(如本题错解)，特别是诱导公式右边的符号要记准．[错因分析]对诱导公式三角函数值的符号确定掌握不好，在sin[3π2－(π4－α)]中，要把“π4－α”看成锐角来确定三角函数值符号．[思路分析]诱导公式共有六组公式，公式较多，易错记错用(如本题错解)，特别是诱导公式右边的符号要记准．第一章三角函数[正解]∵0<α<π2，∴－π4<π4－α<π4，∴cos(π4－α)>0，∴cos(π4－α)＝1－sin2π4－α＝1－a2，sin(5π4＋α)＝sin[π＋(π4＋α)]＝－sin(π4＋α)＝－cos[π2－(π4－α)]＝－cos(π4－α)＝－1－a2.[误区警示]在公式“奇变偶不变，符号看象限”中角可以单角，也可以是一个复角．[正解]∵0<α<π2，∴－π4<π4－α<π4，∴cos(π4－α)>0，∴cos(π4－α)＝1－sin2π4－α＝1－a2，sin(5π4＋α)＝sin[π＋(π4＋α)]＝－sin(π4＋α)＝－cos[π2－(π4－α)]＝－cos(π4－α)＝－1－a2.[误区警示]在公式“奇变偶不变，符号看象限”中角可以单角，也可以是一个复角．第一章三角函数〔跟踪练习4〕已知cos(π＋α)＝－12，求cos(π2＋α)的值．[解析]∵cos(π＋α)＝－cosα＝－12，∴cosα＝12，∴α为第一或第四象限角．①若α为第一象限角，则cos(π2＋α)＝－sinα＝－1－cos2α＝－1－122＝－32.②若α为第四象限角，则cos(π2＋α)＝－sinα＝1－cos2α＝1－122＝32.〔跟踪练习4〕已知cos(π＋α)＝－12，求cos(π2＋α)的值．[解析]∵cos(π＋α)＝－cosα＝－12，∴cosα＝12，∴α为第一或第四象限角．①若α为第一象限角，则cos(π2＋α)＝－sinα＝－1－cos2α＝－1－122＝－32.②若α为第四象限角，则cos(π2＋α)＝－sinα＝1－cos2α＝1－122＝32.第一章三角函数课堂达标验收1．若cos65°＝a，则sin25°的值是()A．－aB．aC．1－a2D．－1－a2B[解析]sin25°＝sin(90°－65°)＝cos65°＝a.1．若cos65°＝a，则sin25°的值是()A．－aB．aC．1－a2D．－1－a2[解析]sin25°＝sin(90°－65°)＝cos65°＝a.第一章三角函数2．若sin(π2＋θ)<0，且cos(π2－θ)>0，则θ是()A．第一象限角B．第二象限角C．第三象限角D．第四象限角B[解析]因为cosθ<0，sinθ>0，∴θ是第二象限角．2．若sin(π2＋θ)<0，且cos(π2－θ)>0，则θ是()A．第一象限角B．第二象限角C．第三象限角D．第四象限角[解析]因为cosθ<0，sinθ>0，∴θ是第二象限角．第一章三角函数3．已知cosπ2＋α＝－35，且α是第二象限角，则sinα－3π2的结果是()A．45B．－45C．±45D．35B3．已知cosπ2＋α＝－35，且α是第二象限角，则sinα－3π2的结果是()A．45B．－45C．±45D．35第一章三角函数[解析]∵cosπ2＋α＝－35，∴－sinα＝－35，∴sinα＝35，又α是第二象限角，∴cosα＝－45，∴sinα－3π2＝cosα＝－45.[解析]∵cosπ2＋α＝－35，∴－sinα＝－35，∴sinα＝35，又α是第二象限角，∴cosα＝－45，∴sinα－3π2＝cosα＝－45.第一章三角函数4．若α∈(π，3π2)，则1－sin23π2－α＝()A．sinαB．－sinαC．cosαD．－cosαB[解析]∵α∈(π，32π)，∴sinα<0，∴1－sin232π－α＝1－cos2α＝－sinα.4．若α∈(π，3π2)，则1－sin23π2－α＝()A．sinαB．－sinαC．cosαD．－cosα[解析]∵α∈(π，32π)，∴sinα<0，∴1－sin232π－α＝1－cos2α＝－sinα.第一章三角函数5．(2019·青岛二中高一月考)已知角α的终边上有一点P(1,3)，则sinπ－α－sinπ2＋αcos3π2－α＋2cos－π＋α的值为()A．－25B．－45C．－47D．－4A5．(2019·青岛二中高一月考)已知角α的终边上有一点P(1,3)，则sinπ－α－sinπ2＋αcos3π2－α＋2cos－π＋α的值为()A．－25B．－45C．－47D．－4第一章三角函数[解析]∵角α的终边上有一点P(1,3)，在第一象限，∴由三角函数的定义知sinα＝310，cosα＝110.∵sinπ－α－sinπ2＋αcos32π－α＋2cos－π＋α＝sinα－cosα－sinα－2cosα＝310－110－310－210＝－25.∴选A．[解析]∵角α的终边上有一点P(1,3)，在第一象限，∴由三角函数的定义知sinα＝310，cosα＝110.∵sinπ－α－sinπ2＋αcos32π－α＋2cos－π＋α＝sinα－cosα－sinα－2cosα＝310－110－310－210＝－25.∴选A．感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明栏目导航自主预习学案互动探究学案课时作业学案010203CONTENTS课时作业学案03第一章三角函数谢谢观看必修④·人教A版新课标导学