《一元二次不等式及其解法》高二年级上册PPT课件（第3.2.2课时）.pptx

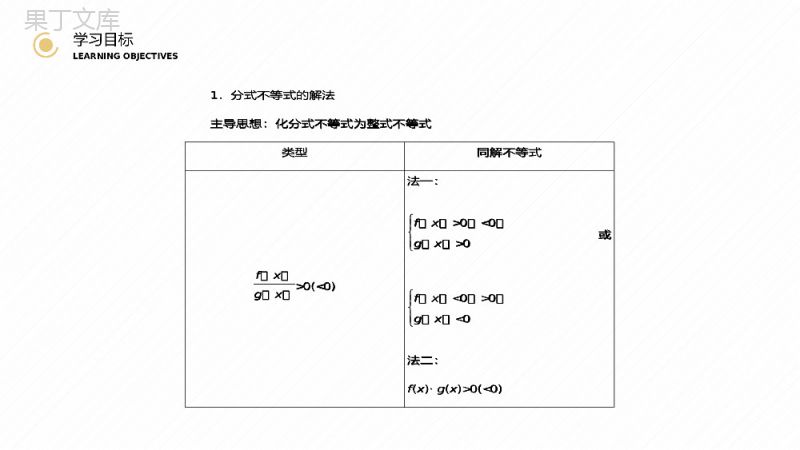
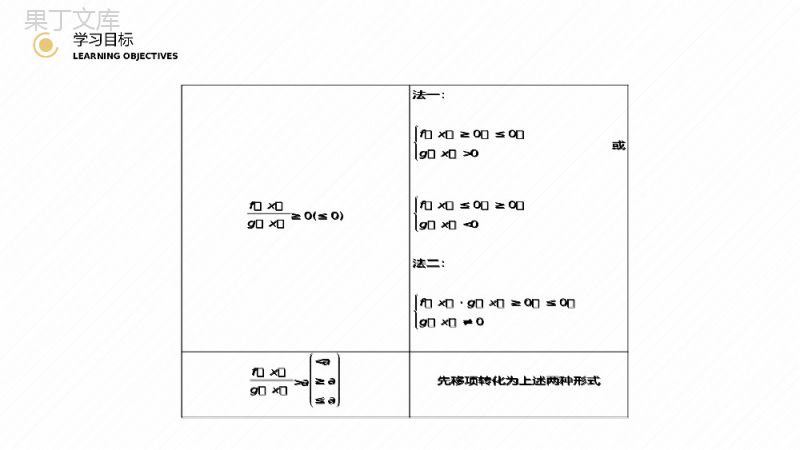
第三章不等式主讲人：办公资源3.2第二课时一元二次不等式及其解法学习目标LEARNINGOBJECTIVES—————————————————————————————————1.掌握一元二次不等式的实际应用(重点).2.理解三个“二次”之间的关系.3.会解一元二次不等式中的恒成立问题(难点)．CONTENTS目录01PART学习目标LEARNINGOBJECTIVES学习目标LEARNINGOBJECTIVES1．分式不等式的解法主导思想：化分式不等式为整式不等式类型同解不等式fxgx>0(<0)法一：fx>0<0gx>0或fx<0>0gx<0法二：f(x)·g(x)>0(<0)1．分式不等式的解法主导思想：化分式不等式为整式不等式类型同解不等式fxgx>0(<0)法一：fx>0<0gx>0或fx<0>0gx<0法二：f(x)·g(x)>0(<0)学习目标LEARNINGOBJECTIVESfxgx≥0(≤0)法一：fx≥0≤0gx>0或fx≤0≥0gx<0法二：fx·gx≥0≤0gx≠0fxgx>a0或fx≤0≥0gx<0法二：fx·gx≥0≤0gx≠0fxgx>a0与(x－3)(x＋2)>0等价吗？将x－3x＋2>0变形为(x－3)(x＋2)>0，有什么好处？[提示]等价；好处是将不熟悉的分式不等式化归为已经熟悉的一元二次不等式．思考：x－3x＋2>0与(x－3)(x＋2)>0等价吗？将x－3x＋2>0变形为(x－3)(x＋2)>0，有什么好处？[提示]等价；好处是将不熟悉的分式不等式化归为已经熟悉的一元二次不等式．学习目标LEARNINGOBJECTIVES2．(1)不等式的解集为R(或恒成立)的条件不等式ax2＋bx＋c>0ax2＋bx＋c<0a＝0b＝0，c>0b＝0，c<0a≠0a>0Δ<0a<0Δ<0(2)有关不等式恒成立求参数的取值范围的方法f(x)≤a恒成立⇔f(x)max≤af(x)≥a恒成立⇔f(x)min≥a2．(1)不等式的解集为R(或恒成立)的条件不等式ax2＋bx＋c>0ax2＋bx＋c<0a＝0b＝0，c>0b＝0，c<0a≠0a>0Δ<0a<0Δ<0(2)有关不等式恒成立求参数的取值范围的方法f(x)≤a恒成立⇔f(x)max≤af(x)≥a恒成立⇔f(x)min≥a学习目标LEARNINGOBJECTIVES思考：x－1>0在区间[2,3]上恒成立的几何意义是什么？区间[2,3]与不等式x－1>0的解集有什么关系？[提示]x－1>0在区间[2,3]上恒成立的几何意义是函数y＝x－1在区间[2,3]上的图象恒在x轴上方．区间[2,3]内的元素一定是不等式x－1>0的解，反之不一定成立，故区间[2,3]是不等式x－1>0的解集的子集．思考：x－1>0在区间[2,3]上恒成立的几何意义是什么？区间[2,3]与不等式x－1>0的解集有什么关系？[提示]x－1>0在区间[2,3]上恒成立的几何意义是函数y＝x－1在区间[2,3]上的图象恒在x轴上方．区间[2,3]内的元素一定是不等式x－1>0的解，反之不一定成立，故区间[2,3]是不等式x－1>0的解集的子集．学习目标LEARNINGOBJECTIVES3．从实际问题中抽象出一元二次不等式模型的步骤：(1)阅读理解，认真审题，分析题目中有哪些已知量和未知量，找准不等关系．(2)设出起关键作用的未知量，用不等式表示不等关系(或表示成函数关系)．(3)解不等式(或求函数最值)．(4)回扣实际问题．思考：解一元二次不等式应用题的关键是什么？3．从实际问题中抽象出一元二次不等式模型的步骤：(1)阅读理解，认真审题，分析题目中有哪些已知量和未知量，找准不等关系．(2)设出起关键作用的未知量，用不等式表示不等关系(或表示成函数关系)．(3)解不等式(或求函数最值)．(4)回扣实际问题．思考：解一元二次不等式应用题的关键是什么？学习目标LEARNINGOBJECTIVES[提示]解一元二次不等式应用题的关键在于构造一元二次不等式模型，选择其中起关键作用的未知量为x，用x来表示其他未知量，根据题意，列出不等关系再求解．[提示]解一元二次不等式应用题的关键在于构造一元二次不等式模型，选择其中起关键作用的未知量为x，用x来表示其他未知量，根据题意，列出不等关系再求解．学习目标LEARNINGOBJECTIVES[基础自测]1．思考辨析(1)不等式1x>1的解集为x<1.()(2)求解m>f(x)恒成立时，可转化为求解f(x)的最小值，从而求出m的范围．()[答案](1)×(2)×提示：(1)1x>1⇒1x－1>0⇒x－1x<0⇒{x0f(x)恒成立转化为m>f(x)max，(2)错．[基础自测]1．思考辨析(1)不等式1x>1的解集为x<1.()(2)求解m>f(x)恒成立时，可转化为求解f(x)的最小值，从而求出m的范围．()[答案](1)×(2)×提示：(1)1x>1⇒1x－1>0⇒x－1x<0⇒{x0f(x)恒成立转化为m>f(x)max，(2)错．学习目标LEARNINGOBJECTIVES2．不等式x＋1x≥5的解集是________．x00在R上恒成立，则实数a的取值范围是________.(0,8)[因为x2－ax＋2a>0在R上恒成立，所以Δ＝a2－4×2a<0，所以00在R上恒成立，则实数a的取值范围是________.(0,8)[因为x2－ax＋2a>0在R上恒成立，所以Δ＝a2－4×2a<0，所以00，y>0，x<40，y<40，xy≥300，整理得y＋x＝40，将y＝40－x代入xy≥300，整理得x2－40x＋300≤0，解得10≤x≤30.]4.在如图3­2­1所示的锐角三角形空地中，欲建一个面积不小于300m2的内接矩形花园(阴影部分)，则其边长x(单位：m)的取值范围是________．图3­2­1[10,30][设矩形高为y，由三角形相似得：x40＝40－y40，且x>0，y>0，x<40，y<40，xy≥300，整理得y＋x＝40，将y＝40－x代入xy≥300，整理得x2－40x＋300≤0，解得10≤x≤30.]02PART合作探究COOPERATIVEINQUIRY合作探究COOPERATIVEINQUIRY分式不等式的解法例1、解下列不等式：(1)x－3x＋2<0；(2)x＋12x－3≤1.分式不等式的解法例1、解下列不等式：(1)x－3x＋2<0；(2)x＋12x－3≤1.合作探究COOPERATIVEINQUIRY[解](1)x－3x＋2<0⇔(x－3)(x＋2)<0⇔－23.即知原不等式的解集为{xx≤－1或x>3}．[跟踪训练]1．解下列不等式：(1)x＋1x－3≥0；(2)5x＋1x＋1<3.[解](1)根据商的符号法则，不等式x＋1x－3≥0可转化成不等式组x＋1x－3≥0，x≠3.解这个不等式组，可得x≤－1或x>3.即知原不等式的解集为{xx≤－1或x>3}．合作探究COOPERATIVEINQUIRY(2)不等式5x＋1x＋1<3可改写为5x＋1x＋1－3<0，即2x－1x＋1<0.可将这个不等式转化成2(x－1)(x＋1)<0，解得－10恒成立，如何求实数a的取值范围？提示：若a＝0，显然f(x)>0不能对一切x∈R都成立．所以a≠0，此时只有二次函数f(x)＝ax2＋2x＋2的图象与直角坐标系中的x轴无交点且抛物线开口向上时，才满足题意，则a＞0Δ＝4－8a<0，解得a>12.不等式恒成立问题[探究问题]1．若函数f(x)＝ax2＋2x＋2对一切x∈R，f(x)>0恒成立，如何求实数a的取值范围？提示：若a＝0，显然f(x)>0不能对一切x∈R都成立．所以a≠0，此时只有二次函数f(x)＝ax2＋2x＋2的图象与直角坐标系中的x轴无交点且抛物线开口向上时，才满足题意，则a＞0Δ＝4－8a<0，解得a>12.合作探究COOPERATIVEINQUIRY2．若函数f(x)＝x2－ax－3对x∈[－3，－1]上恒有f(x)<0成立，如何求a的范围？提示：要使f(x)<0在[－3，－1]上恒成立，则必使函数f(x)＝x2－ax－3在[－3，－1]上的图象在x轴的下方，由f(x)的图象可知，此时a应满足f－3<0，f－1<0，即3a＋6<0，a－2<0，解得a<－2.故当a∈(－∞，－2)时，有f(x)<0在x∈[－3，－1]时恒成立．2．若函数f(x)＝x2－ax－3对x∈[－3，－1]上恒有f(x)<0成立，如何求a的范围？提示：要使f(x)<0在[－3，－1]上恒成立，则必使函数f(x)＝x2－ax－3在[－3，－1]上的图象在x轴的下方，由f(x)的图象可知，此时a应满足f－3<0，f－1<0，即3a＋6<0，a－2<0，解得a<－2.故当a∈(－∞，－2)时，有f(x)<0在x∈[－3，－1]时恒成立．合作探究COOPERATIVEINQUIRY3．若函数y＝x2＋2(a－2)x＋4对任意a∈[－3,1]时，y<0恒成立，如何求x的取值范围？提示：由于本题中已知a的取值范围求x，所以我们可以把函数f(x)转化为关于自变量是a的函数，求参数x的取值问题，则令g(a)＝2x·a＋x2－4x＋4.3．若函数y＝x2＋2(a－2)x＋4对任意a∈[－3,1]时，y<0恒成立，如何求x的取值范围？提示：由于本题中已知a的取值范围求x，所以我们可以把函数f(x)转化为关于自变量是a的函数，求参数x的取值问题，则令g(a)＝2x·a＋x2－4x＋4.合作探究COOPERATIVEINQUIRY要使对任意a∈[－3,1]，y<0恒成立，只需满足g1<0，g－3<0，即x2－2x＋4<0，x2－10x＋4<0.因为x2－2x＋4<0的解集是空集，所以不存在实数x，使函数y＝x2＋2(a－2)x＋4对任意a∈[－3,1]，y<0恒成立．要使对任意a∈[－3,1]，y<0恒成立，只需满足g1<0，g－3<0，即x2－2x＋4<0，x2－10x＋4<0.因为x2－2x＋4<0的解集是空集，所以不存在实数x，使函数y＝x2＋2(a－2)x＋4对任意a∈[－3,1]，y<0恒成立．合作探究COOPERATIVEINQUIRY例3、已知f(x)＝x2＋ax＋3－a，若x∈[－2,2]，f(x)≥0恒成立，求a的取值范围.思路探究：对于含参数的函数在闭区间上的函数值恒大于等于零的问题，可以利用函数的图象与性质求解．[解]设函数f(x)＝x2＋ax＋3－a在x∈[－2,2]时的最小值为g(a)，则(1)当对称轴x＝－a2<－2，即a>4时，g(a)＝f(－2)＝7－3a≥0，解得a≤73，与a>4矛盾，不符合题意．(2)当－a2∈[－2,2]，即－4≤a≤4时，g(a)＝3－a－a24≥0，解得－6≤a≤2，此时－4≤a≤2.(3)当－a2>2，即a<－4时，g(a)＝f(2)＝7＋a≥0，解得a≥－7，此时－7≤a<－4.综上，a的取值范围为－7≤a≤2.例3、已知f(x)＝x2＋ax＋3－a，若x∈[－2,2]，f(x)≥0恒成立，求a的取值范围.思路探究：对于含参数的函数在闭区间上的函数值恒大于等于零的问题，可以利用函数的图象与性质求解．[解]设函数f(x)＝x2＋ax＋3－a在x∈[－2,2]时的最小值为g(a)，则(1)当对称轴x＝－a2<－2，即a>4时，g(a)＝f(－2)＝7－3a≥0，解得a≤73，与a>4矛盾，不符合题意．(2)当－a2∈[－2,2]，即－4≤a≤4时，g(a)＝3－a－a24≥0，解得－6≤a≤2，此时－4≤a≤2.(3)当－a2>2，即a<－4时，g(a)＝f(2)＝7＋a≥0，解得a≥－7，此时－7≤a<－4.综上，a的取值范围为－7≤a≤2.合作探究COOPERATIVEINQUIRY母题探究：1.(变结论)本例条件不变，若f(x)≥2恒成立，求a的取值范围．[解]若x∈[－2,2]，f(x)≥2恒成立可转化为：当x∈[－2,2]时，f(x)min≥2⇔－a2<－2，fxmin＝f－2＝7－3a≥2或－2≤－a2≤2，fxmin＝f－a2＝3－a－a24≥2或－a2>2，fxmin＝f2＝7＋a≥2，解得a的取值范围为[－5，－2＋22]．母题探究：1.(变结论)本例条件不变，若f(x)≥2恒成立，求a的取值范围．[解]若x∈[－2,2]，f(x)≥2恒成立可转化为：当x∈[－2,2]时，f(x)min≥2⇔－a2<－2，fxmin＝f－2＝7－3a≥2或－2≤－a2≤2，fxmin＝f－a2＝3－a－a24≥2或－a2>2，fxmin＝f2＝7＋a≥2，解得a的取值范围为[－5，－2＋22]．合作探究COOPERATIVEINQUIRY2．(变条件)将例题中的条件“f(x)＝x2＋ax＋3－a，x∈[－2,2]，f(x)≥0恒成立”变为“不等式x2＋2x＋a2－3>0的解集为R”求a的取值范围．[解]法一：∵不等式x2＋2x＋a2－3>0的解集为R，∴函数f(x)＝x2＋2x＋a2－3的图象应在x轴上方，∴Δ＝4－4(a2－3)<0，解得a>2或a<－2.法二：令f(x)＝x2＋2x＋a2－3，要使x2＋2x＋a2－3>0的解集为R，则a满足f(x)min＝a2－4>0，解得a>2或a<－2.法三：由x2＋2x＋a2－3>0，得a2>－x2－2x＋3，即a2>－(x＋1)2＋4，要使该不等式在R上恒成立，必须使a2大于－(x＋1)2＋4的最大值，即a2>4，故a>2或a<－2.2．(变条件)将例题中的条件“f(x)＝x2＋ax＋3－a，x∈[－2,2]，f(x)≥0恒成立”变为“不等式x2＋2x＋a2－3>0的解集为R”求a的取值范围．[解]法一：∵不等式x2＋2x＋a2－3>0的解集为R，∴函数f(x)＝x2＋2x＋a2－3的图象应在x轴上方，∴Δ＝4－4(a2－3)<0，解得a>2或a<－2.法二：令f(x)＝x2＋2x＋a2－3，要使x2＋2x＋a2－3>0的解集为R，则a满足f(x)min＝a2－4>0，解得a>2或a<－2.法三：由x2＋2x＋a2－3>0，得a2>－x2－2x＋3，即a2>－(x＋1)2＋4，要使该不等式在R上恒成立，必须使a2大于－(x＋1)2＋4的最大值，即a2>4，故a>2或a<－2.03PART当堂达标REACHINGTHEGOALINCOURT当堂达标REACHINGTHEGOALINCOURT1．（2019年厦门模拟）若集合A＝{x－1≤2x＋1≤3}，B＝xx－2x≤0，则A∩B等于()A．{x－1≤x<0}B．{x00时，相应二次方程中的Δ＝a2－4a≤0，得{a00时，相应二次方程中的Δ＝a2－4a≤0，得{a00的解集为________．【答案】{x－4－1}[原式可转化为(x＋1)(x＋2)2(x＋3)(x＋4)>0，根据数轴穿根法，解集为－4－1.]3．不等式x＋1x＋22x＋3x＋4>0的解集为________．【答案】{x－4－1}[原式可转化为(x＋1)(x＋2)2(x＋3)(x＋4)>0，根据数轴穿根法，解集为－4－1.]当堂达标REACHINGTHEGOALINCOURT4．（2019年屯溪区校级月考）设x2－2x＋a－8≤0对于任意x∈(1,3)恒成立，则a的取值范围是________.【答案】(－∞，5][原不等式x2－2x＋a－8≤0转化为a≤－x2＋2x＋8对任意x∈(1,3)恒成立，设f(x)＝－x2＋2x＋8，易知f(x)在[1,3]上的最小值为f(3)＝5.∴a∈(－∞，5]．]4．（2019年屯溪区校级月考）设x2－2x＋a－8≤0对于任意x∈(1,3)恒成立，则a的取值范围是________.【答案】(－∞，5][原不等式x2－2x＋a－8≤0转化为a≤－x2＋2x＋8对任意x∈(1,3)恒成立，设f(x)＝－x2＋2x＋8，易知f(x)在[1,3]上的最小值为f(3)＝5.∴a∈(－∞，5]．]感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明当堂达标REACHINGTHEGOALINCOURT5．（2019年慈溪市模拟）某文具店购进一批新型台灯，若按每盏台灯15元的价格销售，每天能卖出30盏；若售价每提高1元，日销售量将减少2盏．为了使这批台灯每天能获得400元以上的销售收入，应怎样制定这批台灯的销售价格？【答案】设每盏台灯售价x元，则x≥15，并且日销售收入为x[30－2(x－15)]，由题意知，当x≥15时，有x[30－2(x－15)]>400，解得：15≤x<20.所以为了使这批台灯每天获得400元以上的销售收入，应当制定这批台灯的销售价格为x∈[15,20)．5．（2019年慈溪市模拟）某文具店购进一批新型台灯，若按每盏台灯15元的价格销售，每天能卖出30盏；若售价每提高1元，日销售量将减少2盏．为了使这批台灯每天能获得400元以上的销售收入，应怎样制定这批台灯的销售价格？【答案】设每盏台灯售价x元，则x≥15，并且日销售收入为x[30－2(x－15)]，由题意知，当x≥15时，有x[30－2(x－15)]>400，解得：15≤x<20.所以为了使这批台灯每天获得400元以上的销售收入，应当制定这批台灯的销售价格为x∈[15,20)．第三章不等式主讲人：办公资源3.2第一课时谢谢倾听