专题提升(十三)-以圆为背景的相似三角形的计算与证明

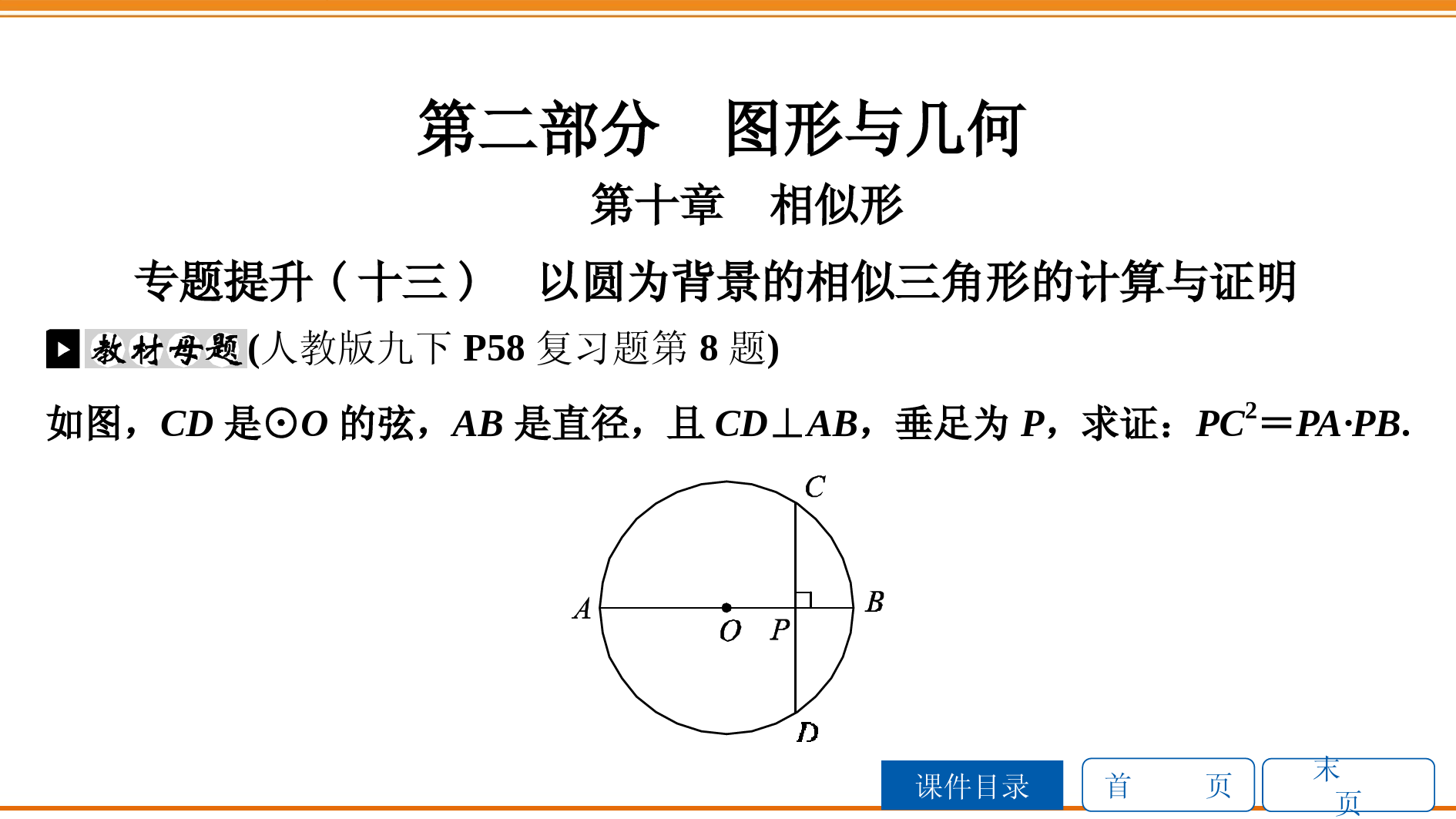
首页课件目录末页第二部分图形与几何第十章相似形专题提升(十三)以圆为背景的相似三角形的计算与证明(人教版九下P58复习题第8题)如图，CD是⊙O的弦，AB是直径，且CD⊥AB，垂足为P，求证：PC2＝PA·PB.首页课件目录末页证明：如答图，连接AC，BD.∵∠A＝∠D，∠C＝∠B，∴△APC∽△DPB.∴PCPB＝PAPD.∴PC·PD＝PA·PB.∵AB是直径，CD⊥AB，∴PC＝PD.∴PC2＝PA·PB.首页课件目录末页【思想方法】证明等积式的常用方法是把等积式转化为比例式，一般要证明比例式，就要证明三角形相似．证明圆中的相似三角形时，要充分运用切线的性质、圆周角定理及推论、垂径定理等知识点．首页课件目录末页1．[2019·宜宾]如图，线段AB经过⊙O的圆心O，交⊙O于A，C两点，BC＝1，AD为⊙O的弦，连接BD，∠BAD＝∠ABD＝30°，连接DO并延长交⊙O于点E，连接BE交⊙O于点M.(1)求证：直线BD是⊙O的切线；(2)求⊙O的半径OD的长；(3)求线段BM的长．首页课件目录末页(1)证明：∵OA＝OD，∠A＝∠ABD＝30°，∴∠A＝∠ADO＝30°，∴∠DOB＝∠A＋∠ADO＝60°，∴∠ODB＝180°－∠DOB－∠ABD＝90°.∵OD是半径，∴BD是⊙O的切线．首页课件目录末页(2)解：∵∠ODB＝90°，∠DBC＝30°，∴OD＝12OB.∵OC＝OD，∴OD＝OC＝BC＝1，∴⊙O的半径OD的长为1.首页课件目录末页(3)解：∵OD＝1，∴DE＝2，BD＝3，∴BE＝BD2＋DE2＝7.连接DM(图略)，则有DM⊥EB，易证△EBD∽△DBM.∴DBEB＝BMBD.∴BM＝BD2BE＝37＝377.首页课件目录末页2．[2019·苏州节选]如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，BC与AD，OD分别交于点E，F.求证：(1)DO∥AC；(2)DE·DA＝DC2.首页课件目录末页证明：(1)∵点D是BC︵的中点，OD是圆的半径，∴OD⊥BC.∵AB是圆的直径，∴∠ACB＝90°，∴DO∥AC.首页课件目录末页(2)∵CD︵＝BD︵，∴∠CAD＝∠DCB，即∠CAD＝∠ECD，∴△DCE∽△DAC，∴CDAD＝DEDC，∴CD2＝DE·DA.首页课件目录末页3．[2019·聊城]如图，△ABC内接于⊙O，AB为直径，作DO⊥AB于点O，延长BC，OD交于点F，过点C作⊙O的切线CE，交OF于点E.(1)求证：EC＝ED；(2)如果OA＝4，EF＝3，求弦AC的长．首页课件目录末页(1)证明：如答图，连接OC.∵CE与⊙O相切，OC是⊙O的半径，∴OC⊥CE，∴∠OCA＋∠ACE＝90°.∵OA＝OC，∴∠A＝∠OCA，∴∠ACE＋∠A＝90°.∵OD⊥AB，∴∠ODA＋∠A＝90°.∴∠ODA＝∠ACE.∵∠ODA＝∠CDE，∴∠CDE＝∠ACE，∴EC＝ED.首页课件目录末页(2)解：∵AB为直径，∴∠ACB＝90°.在Rt△DCF中，∠DCE＋∠ECF＝90°，∠DCE＝∠CDE，∴∠CDE＋∠ECF＝90°.∵∠CDE＋∠F＝90°，∴∠ECF＝∠F，∴EC＝EF.∵EF＝3，∴EC＝DE＝3.首页课件目录末页在Rt△OCE中，OC＝4，CE＝3，∴OE＝OC2＋EC2＝5，∴OD＝OE－DE＝2.在Rt△OAD中，AD＝OA2＋OD2＝25.在Rt△AOD和Rt△ACB中．首页课件目录末页∵∠A＝∠A，∴Rt△AOD∽Rt△ACB，∴AOAC＝ADAB，即4AC＝258，∴AC＝1655.首页课件目录末页4．[2018·泸州]如图，已知AB，CD是⊙O的直径，过点C作⊙O的切线，交AB的延长线于点P，⊙O的弦DE交AB于点F，且DF＝EF.(1)求证：CO2＝OF·OP；(2)连接EB，交CD于点G，过点G作GH⊥AB于点H，若PC＝42，PB＝4，求GH的长．首页课件目录末页(1)证明：在⊙O中，DF＝EF，AB为直径，∴AB⊥ED.∵CP与⊙O相切于点C，∴OC⊥CP.∴∠OFD＝∠OCP＝90°.又∵∠FOD＝∠COP，∴△OFD∽△OCP.首页课件目录末页∴OFOC＝ODOP.∴OC·OD＝OF·OP.∵OC＝OD，∴CO2＝OF·OP.首页课件目录末页(2)解：∵PC＝42，PB＝4，在Rt△PCO中，PC2＋CO2＝PO2，即(42)2＋CO2＝(4＋CO)2，解得CO＝2.∴OP＝PB＋OB＝PB＋CO＝6.由(1)知CO2＝OF·OP，首页课件目录末页∴22＝6OF.∴OF＝23.易证△GHO∽△DFO，∴GHDF＝HOFO.易证△GHB∽△EFB，∴GHEF＝HBFB.∴HOFO＝HBFB，首页课件目录末页即HO23＝2－HO2＋23.解得HO＝25.易证△OHG∽△OCP，∴OHOC＝GHPC，即252＝GH42.解得GH＝425.首页课件目录末页5．[2019·绵阳]如图，AB是⊙O的直径，点C为BD︵的中点，CF为⊙O的弦，且CF⊥AB，垂足为点E，连接BD交CF于点G，连接CD，AD，BF.(1)求证：△BFG≌△CDG；(2)若AD＝BE＝2，求BF的长．首页课件目录末页5．[2019·绵阳]如图，AB是⊙O的直径，点C为BD︵的中点，CF为⊙O的弦，且CF⊥AB，垂足为点E，连接BD交CF于点G，连接CD，AD，BF.(1)求证：△BFG≌△CDG；(2)若AD＝BE＝2，求BF的长．首页课件目录末页(1)证明：∵C是BC︵的中点，∴CD︵＝BC︵，∴∠F＝∠CDG.∵AB是⊙O的直径，且CF⊥AB，∴BC︵＝BF︵，∴CD︵＝BF︵，∴CD＝BF，在△BFG和△CDG中．首页课件目录末页∵∠F＝∠CDG，∠FGB＝∠DGC，BF＝CD，∴△BFG≌△CDG(AAS)．首页课件目录末页(2)解：如答图，过点C作CH⊥AD交延长线于点H，连接AC，BC，∵CD︵＝BC︵，∴∠HAC＝∠BAC.∵CE⊥AB，易证Rt△AHC≌Rt△AEC(AAS)，∴AE＝AH，CH＝CE.又∵CD＝CB，首页课件目录末页∴Rt△CDH≌Rt△CBE(HL)，∴DH＝BE＝2，∴AE＝AH＝2＋2＝4，∴AB＝4＋2＝6.∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ACB＝∠CEB＝90°.首页课件目录末页∵∠EBC＝∠CBA，∴△BEC∽△BCA，∴BCBA＝BEBC，∴BC2＝AB·BE＝6×2＝12，∴BF＝BC＝23.首页课件目录末页6．[2019·黄石]如图，AB是⊙O的直径，点D在AB的延长线上，C，E是⊙O上的两点，CE＝CB，∠BCD＝∠CAE，延长AE交BC的延长线于点F.(1)求证：CD是⊙O的切线；(2)求证：CE＝CF；(3)若BD＝1，CD＝2，求弦AC的长．首页课件目录末页(1)证明：如答图，连接OC.∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAD＋∠ABC＝90°.∵CE＝CB，∴∠CAE＝∠CAB.∵∠BCD＝∠CAE，∴∠CAB＝∠BCD.首页课件目录末页∵OB＝OC，∴∠OBC＝∠OCB，∴∠OCB＋∠BCD＝∠CAB＋∠ABC＝90°，∴∠OCD＝90°，∴CD是⊙O的切线．首页课件目录末页(2)证明：∵∠BAC＝∠FAC，∠ACB＝∠ACF＝90°，AC＝AC，∴△ABC≌△AFC(ASA)，∴CB＝CF.又∵CB＝CE，∴CE＝CF.首页课件目录末页(3)解：∵∠BCD＝∠CAD，∠D＝∠D，∴△CBD∽△ACD，∴CDBD＝ADCD＝ACCB，∴21＝AD2＝ACBC，∴DA＝2，AC＝2BC.∴AB＝AD－BD＝2－1＝1.首页课件目录末页设BC＝a，则AC＝2a.由勾股定理可得a2＋(2a)2＝12，解得a＝33.∴AC＝63.首页课件目录末页7．[2018·遂宁]如图，过⊙O外一点P作⊙O的切线PA切⊙O于点A，连接PO并延长，与⊙O交于C，D两点，M是半圆CD的中点，连接AM，交CD于点N，连接AC，CM.(1)求证：CM2＝MN·MA；(2)若∠P＝30°，PC＝2，求CM的长．首页课件目录末页(1)证明：∵在⊙O中，M是半圆CD的中点，∴∠CAM＝∠DCM，即∠CAM＝∠NCM.又∵∠M是公共角，∴△CMN∽△AMC.∴CMAM＝MNMC.∴CM2＝MN·MA.首页课件目录末页(2)解：如答图，连接OA，DM.∵PA是⊙O的切线，∴∠PAO＝90°.又∵∠P＝30°，∴OA＝12PO＝12(PC＋CO)．设⊙O的半径为r，∵PC＝2，∴r＝12(2＋r)．首页课件目录末页解得r＝2.又∵CD是直径，∴∠CMD＝90°.∵M是半圆CD的中点，∴CM＝DM.∴△CMD是等腰直角三角形．在Rt△CMD中，由勾股定理，得CM2＋DM2＝CD2，即2CM2＝16.解得CM＝22.首页课件目录末页8．[2019·泰州]如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为弧AC的中点，过点D作DE∥AC，交BC的延长线于点E.(1)判断DE与⊙O的位置关系，并说明理由；(2)若⊙O的半径为5，AB＝8，求CE的长．首页课件目录末页解：(1)DE为⊙O的切线，理由如下：如答图，连接OD.∵AC为⊙O的直径，D为弧AC的中点，∴AD︵＝CD︵，∴AD＝DC.∵AO＝OC，∴OD⊥AC，∴∠AOD＝∠COD＝90°.又∵DE∥AC，∴∠EDO＝∠AOD＝90°，∴OD⊥DE，∴DE为⊙O的切线．首页课件目录末页(2)∵DE∥AC，∴∠EDC＝∠ACD.∵∠ACD＝∠ABD，∴∠EDC＝∠DBA.又∵∠DCE＝∠BAD，∴△DCE∽△BAD，CEAD＝DCBA.∵半径为5，∴AC＝10.∵D为弧AC的中点，∴AD＝CD＝52，∴CE＝254.首页课件目录末页如图，AB为⊙O的直径，CD与⊙O相切于点C，且OD⊥BC，垂足为F，OD交⊙O于点E.求证：(1)∠D＝∠AEC；(2)OA2＝OD·OF.首页课件目录末页证明：(1)如答图，连接OC.∵CD与⊙O相切于点C，∴∠OCD＝90°.∴∠OCB＋∠DCF＝90°.又∵∠D＋∠DCF＝90°，∴∠OCB＝∠D.∵OB＝OC，∴∠OCB＝∠B.又∵∠B＝∠AEC，∴∠D＝∠AEC.首页课件目录末页(2)∵∠B＝∠AEC，∠D＝∠AEC，∴∠D＝∠B.∵OD⊥BC，∴∠BFO＝∠DCO＝90°.∴△DOC∽△BOF，∴OCOF＝ODOB，即OAOF＝ODOA.∴OA2＝OD·OF.