专题提升(十一)-以特殊四边形为背景的计算与证明

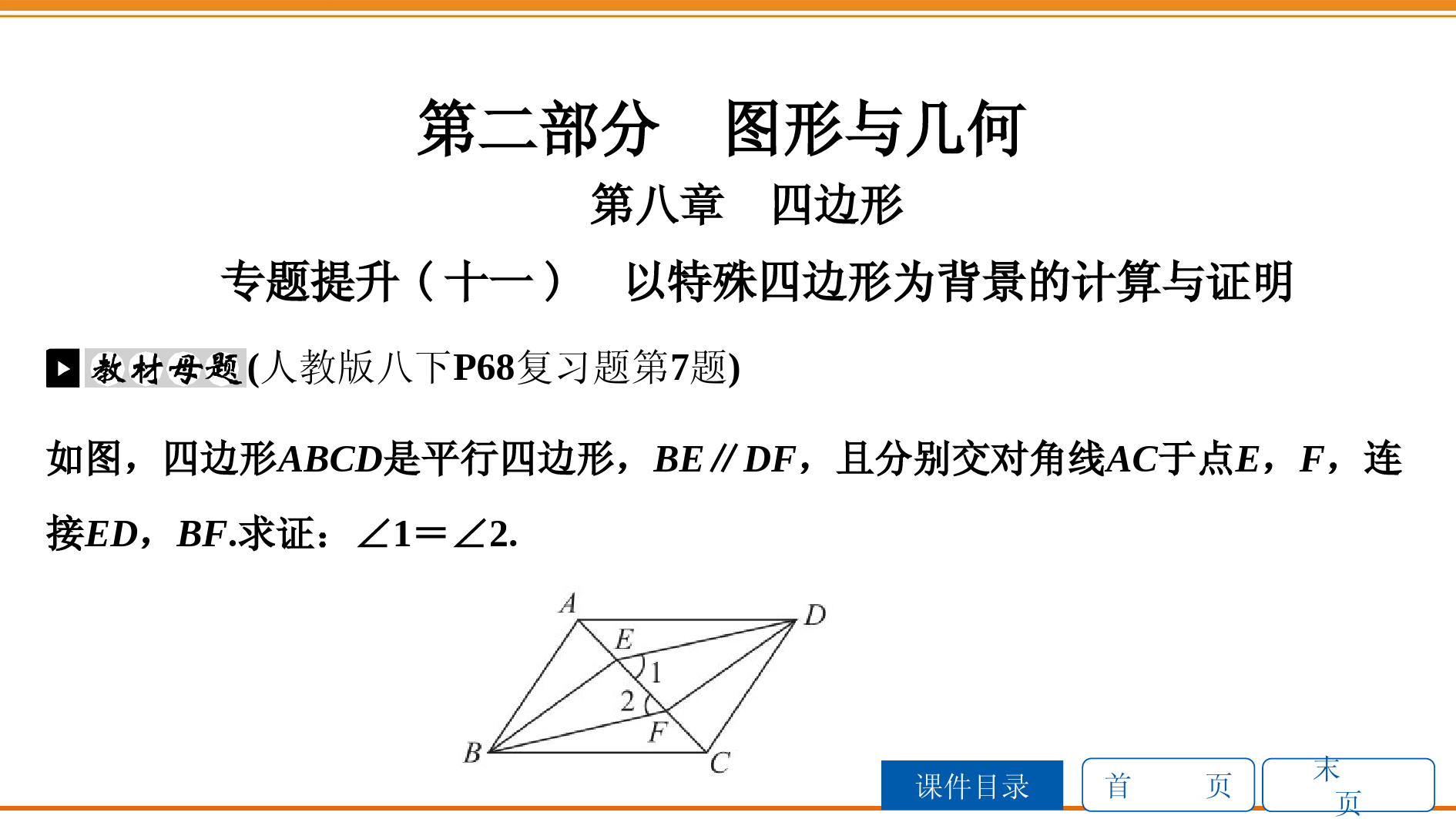
首页课件目录末页第二部分图形与几何第八章四边形专题提升(十一)以特殊四边形为背景的计算与证明(人教版八下P68复习题第7题)如图，四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接ED，BF.求证：∠1＝∠2.首页课件目录末页证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∴∠BAE＝∠DCF.又∵BE∥DF，∴∠BEF＝∠DFE.∵∠BEF＋∠AEB＝180°，∠DFE＋∠CFD＝180°，∴∠AEB＝∠CFD.∴△ABE≌△CDF(AAS)．首页课件目录末页∴BE＝DF.又∵BE∥DF，∴四边形BFDE是平行四边形．∴DE∥BF.∴∠1＝∠2.首页课件目录末页【思想方法】平行四边形是一种特殊的四边形，它具有对边平行且相等、对角线互相平分等性质．根据平行四边形的性质，可以解决一些有关的计算或证明问题．平行四边形的判定有四种常用方法：两组对边分别平行；两组对边分别相等；一组对边平行且相等；对角线互相平分．首页课件目录末页[2018·恩施州]如图，点B，F，C，E在一条直线上，FB＝CE，AB∥ED，AC∥FD，AD交BE于点O.求证：AD与BE互相平分．首页课件目录末页证明：如答图，连接BD，AE.∵AB∥ED，∴∠ABC＝∠DEF.∵AC∥FD，∴∠ACB＝∠DFE.∵FB＝CE，∴BC＝EF.在△ACB和△DFE中，∠ABC＝∠DEF，BC＝EF，∠ACB＝∠DFE，首页课件目录末页∴△ACB≌△DFE(ASA)．∴AB＝DE.又∵AB∥ED，∴四边形ABDE是平行四边形．∴AD与BE互相平分．首页课件目录末页如图，已知E，F分别是▱ABCD的边BC，AD上的点，且BE＝DF.(1)求证：四边形AECF是平行四边形；(2)若四边形AECF是菱形，且BC＝10，∠BAC＝90°，求BE的长．首页课件目录末页(1)证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC.∵BE＝DF，∴AD－DF＝BC－BE，即AF＝EC.∴四边形AECF是平行四边形．首页课件目录末页(2)解：如答图，∵四边形AECF是菱形，∴AE＝EC.∴∠1＝∠2.∵∠BAC＝90°，∴∠3＝90°－∠2，∠4＝90°－∠1.∴∠3＝∠4.∴AE＝BE.∴BE＝AE＝CE＝12BC＝5.首页课件目录末页类型之二以矩形、菱形或正方形为背景的计算与证明(人教版八下P64数学活动1)如果我们身旁没有量角器或三角板，又需要作60°，30°，15°等大小的角，可以采用下面的方法(如图)：首页课件目录末页(1)对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；(2)再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM.同时，得到了线段BN，MN，再把纸片展平．观察所得的∠ABM，∠MBN和∠NBC，这三个角有什么关系？你能证明吗？首页课件目录末页解：∠ABM＝∠MBN＝∠NBC＝30°.证明如下：由题意知，△AMB≌△NMB，∠MAB＝∠MNB＝90°，∴∠ABM＝∠MBN.教材母题答图如答图，延长MN，交BC于点G.首页课件目录末页∵∠MNB＝90°，∴∠BNG＝90°.又∵EF∥BC，AE＝BE，∴MN＝GN.在△MNB与△GNB中，MN＝GN，∠MNB＝∠GNB，BN＝BN，首页课件目录末页∴△MNB≌△GNB(SAS)．∴∠MBN＝∠GBN.又∵∠ABM＋∠MBN＋∠NBC＝90°，∴∠ABM＝∠MBN＝∠NBC＝30°.【思想方法】折叠的本质是轴对称，折叠在实际生活中有广泛的应用，折叠前后的图形全等是解题的关键．特殊四边形与折叠的结合能很好地考查学生综合运用知识的能力，是中考的热点考题．首页课件目录末页1．[2018·荆州]如图，对折矩形纸片ABCD，使AB与DC重合，得到折痕MN，将纸片展平；再一次折叠，使点D落到MN上的点F处，折痕AP交MN于点E，延长PF，交AB于点G.求证：(1)△AFG≌△AFP；(2)△APG为等边三角形．首页课件目录末页证明：(1)由对折，得MN∥AB，且M，N分别为AD，BC的中点．∴EF∥AG，E，F分别为PA，PG的中点．∴PF＝GF.由折叠的性质，得∠PFA＝∠D＝90°.∴∠GFA＝90°.首页课件目录末页在△AFG和△AFP中，GF＝PF，∠GFA＝∠PFA，AF＝AF，∴△AFG≌△AFP(SAS)．首页课件目录末页(2)∵△AFG≌△AFP，∴AP＝AG，∠2＝∠3.又∵∠2＝∠1，∴∠1＝∠2＝∠3.又∵∠1＋∠2＋∠3＝90°，∴∠1＝∠2＝∠3＝30°，∠PAG＝∠2＋∠3＝60°.∴△APG为等边三角形．首页课件目录末页2．[2019·青岛]如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至点G，使EG＝AE，连接CG.(1)求证：△ABE≌△CDF；(2)当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．首页课件目录末页(1)证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，OB＝OD，OA＝OC，∴∠ABE＝∠CDF.∵点E，F分别为OB，OD的中点，∴BE＝12OB，DF＝12OD，∴BE＝DF.首页课件目录末页在△ABE和△CDF中，AB＝CD，∠ABE＝∠CDF，BE＝DF，∴△ABE≌△CDF(SAS)．首页课件目录末页(2)解：当AC＝2AB时，四边形EGCF是矩形；理由如下：∵AC＝2OA，AC＝2AB，∴AB＝OA.∵E是OB的中点，∴AG⊥OB，∴∠OEG＝90°，同理可得：∠OFC＝90°，∴AG∥CF，即EG∥CF.首页课件目录末页∵EG＝AE，OA＝OC，∴OE是△AGC的中位线，∴EO∥GC，∴EF∥GC，∴四边形EGCF是平行四边形．∵∠OEG＝90°，∴四边形EGCF是矩形．首页课件目录末页3．[2019·宁波]如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．(1)求证：BG＝DE；(2)若E为AD中点，FH＝2，求菱形ABCD的周长．首页课件目录末页(1)证明：在矩形EFGH中，EH＝GF，EH∥FG，∠GFH＝∠EHF，∠BFG＝180°－∠GFH，∠DHE＝180°－∠EHF，∴∠BFG＝∠DHE.在菱形ABCD中，AD∥BC，∠GBF＝∠EDH，∴△BGF≌△DEH(AAS)，∴BG＝DE.首页课件目录末页(2)解：如答图，连接EG.在菱形ABCD中，AD∥BC，AD＝BC.∵E为AD中点，AE＝ED，BG＝DE，∴AE＝BG，∴四边形ABGE是平行四边形，∴AB＝EG.在矩形EFGH中，EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长为8.首页课件目录末页4．[2019·鄂州]如图，在矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB，CD边于点E，F.(1)求证：四边形DEBF是平行四边形；(2)当DE＝DF时，求EF的长．首页课件目录末页(1)证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠DFO＝∠BEO.又∵∠DOF＝∠BOE，OD＝OB，∴△DOF≌△BOE(AAS)，∴DF＝BE.又∵DF∥BE，∴四边形DEBF是平行四边形．首页课件目录末页(2)解：∵DE＝DF，且四边形DEBF是平行四边形，∴四边形DEBF是菱形，∴DE＝BE，EF⊥BD，OE＝OF，设AE＝x，则DE＝BE＝8－x.在Rt△ADE中，根据勾股定理，得AE2＋AD2＝DE2，∴x2＋62＝(8－x)2，首页课件目录末页解得x＝74.∴DE＝8－74＝254.在Rt△ABD中，根据勾股定理，得AB2＋AD2＝BD2，∴BD＝62＋82＝10，首页课件目录末页∴OD＝12BD＝5.在Rt△DOE中，根据勾股定理，得DE2－OD2＝OE2，∴OE＝2542－52＝154，∴EF＝2OE＝152.首页课件目录末页如图，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E，F分别在菱形的边BC，CD上滑动，且点E，F不与点B，C，D重合．(1)求证：不论E，F在BC，CD上如何滑动，总有BE＝CF；(2)当点E，F在BC，CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化．如果不变，求出其定值；如果变化，求出其最大(或最小)值．首页课件目录末页(1)证明：如答图，连接AC.∵在菱形ABCD中，∠BAD＝120°，∴∠BAC＝60°，∠B＝60°.∴△ABC是正三角形．∴AB＝AC.∵△AEF为正三角形，∴∠EAF＝60°，AE＝AF.首页课件目录末页∴∠BAC＝∠EAF，∴∠BAC－∠EAC＝∠EAF－∠EAC，即∠BAE＝∠CAF.∴△ABE≌△ACF(SAS)．∴BE＝CF.首页课件目录末页(2)解：当E，F在BC，CD上滑动时，四边形AECF的面积不发生变化，其值为43.△CEF的面积发生变化，其最大值为3.由(1)知S△ABE＝S△ACF，∴S四边形AECF＝S△AEC＋S△ACF＝S△AEC＋S△ABE＝S△ABC＝4×23×12＝43.∵S△CEF＝S四边形AECF－S△AEF＝43－34AE2，首页课件目录末页当AE⊥BC时，AE的长最小，最小值为32AB，此时△CEF的面积取得最大值，∵AEmin＝32×4＝23，∴S△CEF的最大值为43－34×(23)2＝3.