线性规划问题,线性规划问题化为标准形式例题

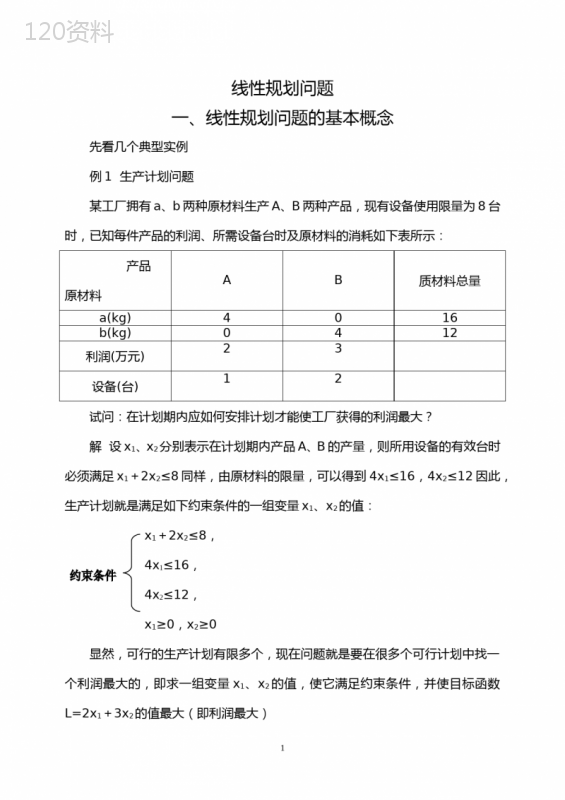
('线性规划问题一、线性规划问题的基本概念先看几个典型实例例1生产计划问题某工厂拥有a、b两种原材料生产A、B两种产品，现有设备使用限量为8台时，已知每件产品的利润、所需设备台时及原材料的消耗如下表所示：产品原材料AB质材料总量a(kg)4016b(kg)0412利润(万元)23设备(台)12试问：在计划期内应如何安排计划才能使工厂获得的利润最大？解设x1、x2分别表示在计划期内产品A、B的产量，则所用设备的有效台时必须满足x1＋2x2≤8同样，由原材料的限量，可以得到4x1≤16，4x2≤12因此，生产计划就是满足如下约束条件的一组变量x1、x2的值：x1＋2x2≤8，4x1≤16，4x2≤12，x1≥0，x2≥0显然，可行的生产计划有限多个，现在问题就是要在很多个可行计划中找一个利润最大的，即求一组变量x1、x2的值，使它满足约束条件，并使目标函数L=2x1＋3x2的值最大（即利润最大）1例2资金分配问题某商店拥有100万元资金，准备经营A、B、C三种商品，其中A商品有A1、A2两种型号，B商品有B1、B2两种型号，每种商品的利润率如下表所示：商品ABCA1A2B1B2利润率（%）7.310.36.47.54.5在经营中有以下限制：(1)经营A或B的资金各自都不能超过总资金的50%；(2)经营C的资金不能少于经营B的资金的25%；(3)经营A2的资金不能超过经营A的总资金的60%；试问应怎样安排资金的使用才能使利润最大？解设经营A1、A2、B1、B2、C的资金分别为x1，x2,x3,x4，x5（万元），这一问题的数学模型为求一组变量x1、x2，…，x5的值，使它满足x1＋x2＋…＋x5=100，x1＋x2≤50，x3＋x4≤50，025x3＋0.25x4－x5≤00.6x1－0.4x2≥0，xj≥0（j=1，2，…，5）并使目标函数L=0.073x1＋0.103x2＋0.064x4＋0.075x4＋0.045x5的值最大(利润最大)上面我们建立了几个实际问题的数学模型，虽然实际问题各不相同，但是它2们的数学模型却有相同的数学形式，这就是：表示约束条件的数学式子都是线性等式或线性不等式，表示问题最优化指标的目标函数都是线性函数，因为约束条件和目标函数都是线性的，所以把具有这种模型的问题称为线性规划问题。线性规划问题的数学模型的一般形式是Max(Min)L=c1x1＋c2x2＋…＋cnxn.(1)a11x1＋a12x2＋…＋a1nxn≤b1(或≥b1，或=b1),a21x1＋a22x2＋…＋a2nxn≤b2(或≥b2，或=b2),………………………………(2)am1x1＋am2x2＋…＋amnxn≤bm(或≥bm，或=bm)，xj≥（j=1，2，…，n）.(3)即求一组变量xj（j=1，2，…，n）的值，满足约束条件，使目标函数L的值最大（或最小），其中，x1，x2，…，xn称为决策变量，简称变量，约束条件（3）称为变量的非负约束。满足约束条件的一组变量的值称为线性规划问题的一个可行解，使目标函数L取得取大值（或最小值）的可行解称为最优解，此时，目标函数的值称为最优值，“s.t.”表示约束条件。例如，在例1中，若变量x1，x2取值为x1=1，x2=2时，它们满足约束条件，因此x1=1，x2=2是该问题的一个可行解，此时目标函数的值为8。求解线性规划问题有不少现成的数学软件，LINDO软件就是其中之一，在LINDO6.1版本下打开，直接输入数学模型，例如，输入倒1的模型Max2X1＋3X2s.t.X1＋2X2＜=834X1＜=164X2＜=12end注：LINDO中已规定所有决策变量均为非负，因此不必输入约束条件中的非负约束条件，程序最后以“end”结束将文件存储并命名后，选择菜单“Solve”，得输出OBJECTIVEFUNCTIONVALUE1)14.000000VARIABLEVALUEREDUCEDCOSTX14.000000X22.000000即，生产A产品4件、B产品2件，利润为14万元。例3工作选择人员设有A1、A2、A3、A4四个人完成B1、B2、B3、B4四项工作，每人只做一件工作且每件工作仅由一人担任，Ai完成工作Bj所需时间为Cij（i，j=1，2，3，4）（单位：天），如下表所示。BjCijAiB1B2B3B4A18131823A210141627A32102126A414222628试问应指派哪个人去承担哪件工作，才能使总的花费时间最少？这个问题与上述各例有所不同，上述各例所设的变量都是问题中所要求的数量，而这个例题中我们要引入的变量必须具有指定某人做某件工作，而其他人不能做该工作。数0、1就起到了这种作用，变量取1，说明该人做这件事，在总的4花费时间中贡献时间，变量取0表示不做这件事，从而在总的花费时间中不作出贡献。解引入16个变量1，当指派Ai承担工作Bj时；xij=i，j=1，2，3，40，当指派Ai不承担工作Bj时，由于每人只做一件工作，得x11＋x12＋x13＋x14=1x21＋x22＋x23＋x24=1x31＋x32＋x33＋x34=1x41＋x42＋x43＋x44=1由于每件工作仅由一个担任，得x11＋x21＋x31＋x41=1x12＋x22＋x32＋x42=1x13＋x23＋x33＋x43=1x14＋x24＋x34＋x44=1得线性规划模型如下MinT=8x11＋13x12＋18x13＋23x14＋10x21＋14x22＋16x23＋27x24＋2x31＋10x32＋21x33＋26x34＋14x41＋22x42＋26x43＋28x44s.txij=1xij=1i，j=1，2，3，45xij=0或1这种线性规划称为0-1规划，这类问题也称为指派问题将模型输入LINDOMIn8x11＋13x12＋18x13＋23x14＋10x21＋14x22＋16x23＋27x24＋2x31＋10x32＋21x33＋26x34＋14x41＋22x42＋26x43＋28x44s.tx11＋x12＋x13＋x14=1x21＋x22＋x23＋x24=1x31＋x32＋x33＋x34=1x41＋x42＋x43＋x44=1x11＋x21＋x31＋x41=1x12＋x22＋x32＋x42=1x13＋c23＋x33＋x43=1x14＋x24＋x34＋x44=1endint16注：int16表示16个变量全部为0-1变量求解得x12=x23=x31=x44=1,其余xij=0，即A1承担工作B2，A2承担工作B3，A3承担工作B1，A4承担工作B4，花费的总时间最少为59天。例4汽车厂生产计划一汽车厂生产小、中、大三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求、利润以及每月工厂钢材、劳动时间的现有量如下表所示，试制订月生产6计划，使工厂的利润最大。小型中型大型现有量钢材(吨)1.535600劳动时间(小时)28025040060000利润(万元)234解设每月生产小、中、大型汽车的数量分别为x1、x2、x3，工厂的月利润为L，在题目所给参数均不随生产数量变化的假设下，立即可得线性规划模型：MaxL=2x1＋3x2＋4x3s.t1.5x1＋3x2＋5x3≤600280x1＋250x2＋400x3≤60000x1，x2，x3≥0求解得到输出ORJECTIVEFUNCTIONVALUE1）632.2581VARIABLEVALUEREDUCEDCOSTX164.5161290.000000X2167.7419280.000000X30.0000000.946237ROWSLACKORSURPLUSDUALPRICES2)0.0000000.7311833)0.0000000.003226我们看到最优解x1=64.516129,x2=167.741928，x3=0，出现小数，显然不合适对于这个实际问题，变量x1，x2，x3只能取整数，我们必须在上述所建立的线性规划模型中增加约束条件x1，x2，x3为整数7得来的线性规划模型如下：MaxL=4x1＋3x2＋2x3s.t1.5x1＋3x2＋5x3≤600280x1＋25x2＋400x3≤60000x1≥0，x2≥0，x3≥0x1，x2，x3均为整数附加了整数约束条件的线性规划模型称为整数规划用LINDO直接求解，输入文件：max2x1＋3x2＋4x3s.t1.5x1＋3x2＋5x3＜600280x1＋250x2＋400x3＜60000endgin3注：最后一行“gin3”是“3个变量均为整数”的说明语句。求解得到输出（只列出需要的结果）：OBJECTIVEFUNCTIONVALUE1）632.0000VARIABLEVALUEREDUCEDCOSTX164.000000-2.000000X2168.000000-3.000000X30.000000-4.000000最优解为x1=64，x2=168，x3=0，最优值为z=632，即问题要求的月生产计划为生产小型车64辆、中型车168辆，不生产大型车。二、线性规划问题举例8例1自来水输送问题某市有甲、乙、丙、丁四个居民区，自来水由A，B，C三个水库供应，四个区每天必须得到保证的基本生活用水量分别为30，70，10，10千吨，但由于水源紧张，三个水库每天最多只能分别供应50，60，50千吨自来水，由于地理位置的差别，自来水公司从各水库向各区送水所需付出的引水管理费不同（见下表，其中C水库与丁区之间没有输水管道），其他管理费用都是450元/千吨，根据公司规定，各区用户按照统一标准900元/千吨收费，此外，四个区都向公司申请了额外用水量，分别为每天50，70，20，40千吨，该公司应如何分配供水量，才能获利最多？引水管理费(元/千吨)甲乙丙丁A160130220170B140130190150C190200230/问题分析分配供水量就是安排从三个水库向四个区送水的方案，目标是获利最多，而从题目给出的数据看，A，B，C三个水库的供水量160千吨，不超过四个区的基本生活用水量与额外用水量之和300千吨，因而总能全部卖出并获利，于是自来水公司每天的总收入是900×（50＋60＋50）=144000元，与送水方案无关，同样，公司每天的其它管理费用450×（50＋60＋50）=72000元也与送水方案无关，所以，要使利润最大，只需使引水管理费最小即可，另外，送水方案自然要受三个水库的供应量和四个区的需求量的限制。模型建立很明显，决策变量为A，B，C三个水库(i=1，2，3)分别向甲、乙、丙、丁四个区（j=1，2，3，4）的供水量，设水库i向j区的日供水量为xij，由于C水库9与丁区之间没有输水管道，即x34=0,因此只有11个决策变量。由上分析，问题的目标可以从获利最多转化为引水管理费最少，于是有MinL=160x11＋130x12＋220x13＋170x14+140x21＋130x22＋190x23＋150x24＋190x31＋200x32＋230x33约束条件有两类：一类是水库的供应量限制，另一类是各区的需求量限制，由于供水量总能卖出并获利，水库的供应量限制可以表示为x11＋x12＋x13＋x14=50x21＋x22＋x23＋x24=60x31＋x32＋x33=50考虑到各区的基本生活用水量与额外用水量，需求量限制可以表示为30≤x11＋x21＋x31≤8070≤x12＋x22＋x32≤14010≤x13＋x23＋x33≤3010≤x14＋x24≤50再加上决策变量的非负约束模型求解将线性规划模型输入LINDO求解，得到如下输出：OBJECTIVEFUNCTIONVALUE1）24400.00VARIABLEVALUEREDUCEDCOSTX110.00000030.000000X1250.0000000.000000X130.00000050.000000X140.00000020.000000X210.00000010.000000X2250.0000000.00000010X230.00000020.000000X2410.0000000.000000X3140.0000000.000000X320.00000020.000000X3310.0000000.000000即，A水库向乙区供水50千吨，B水库向乙、丁区分别供水50、10千吨，C水库向甲、丙区分别供水40、10千吨，引水管理费为24400元，利润为144000-72000-24400=47600元例2混合泳接力队的选拔问题某班准备从5名游泳队员中选择4人组成接力队，参加学校的4×100m混合泳接力比赛，5名队员4种泳姿的百米平均成绩如下表所示，问应如何选拔队员组成接力队？甲乙丙丁戊蝶泳1＇06〃857〃21＇18〃1＇10〃1＇07〃4仰泳1＇15〃61＇06〃1＇07〃81＇14〃21＇11〃蛙泳1＇27〃1＇06〃41＇24〃61＇09〃61＇23〃8自由泳58〃653〃59〃457〃21＇02〃4问题分析从5名队员中选出4人组成接力队，每人一种泳姿，且4人的泳姿各不相同，使接力队的成绩最好容易想到的一个办法是穷举法，组成接力队的方案共有5！=120种，逐一计算并作比较，即可找出最优方案，显然这不是解决这类问题的好办法，随着问题规模的变大，穷举法的计算量将是无法接受的。可以用0-1变量表示一个队员是否入选接力队，从而建立这个问题的0-1规划模型，借助现成的数学软件求解。11模型建立与求解记甲乙丙丁戊分别为队员i=1，2，3，4，5；记蝶泳、仰泳、蛙泳、自由泳分别为泳姿j=1，2，3，4记队员i的第j种泳姿的百米最好成绩为cij(s)，即有ciji=1i=2i=3i=4i=5j=166.857.2787067.4j=275.66667.874.271j=38766.484.669.683.8j=458.65359.457.262.4引入0-1变量xij，若选择队员i参加泳姿j的比赛，记xij=1，否则记xij=0，根据组成接力队的要求，xij应该满足两个约束条件：第一，每人最多只能入选4种泳姿之一，即对于i=1，2，3，4，5应有xij≤1；第二，每种泳姿必须有1人而且只能有1人入选，即对于j=1，2，3，4，应有xij=1；当队员i入选泳姿j时，cijxij表示他(她)的成绩，否则cijxij=0，于是接力队的成绩可表示为Z=cijxij，这就是该问题的目标函数。综上，这个问题的0-1规划模型可写作MinL=cijxijs.txij≤1，i=1，2，3，4，5xij=1，j=1，2，3，4xij=｛0，1｝模型求解将题目所给数据代人这一模型，并输入LINDO：MIN66.8x11＋75.6x12＋87x13＋58.6x14＋57.2x21＋66x22＋66.4x23＋53x2412＋78x31＋67.8x32＋84.6x33＋59.4x34＋70x41＋74.2x42＋69.6x43＋57.2x44＋67.4x51＋71x52＋83.8x53＋62.4x54s.tx11＋x12＋x13＋x14＜=1x21＋x22＋x23＋x24＜=1x31＋x32＋x33＋x34＜=1x41＋x42＋x43＋x44＜=1x11＋x21＋x31＋x41＋x51=1x12＋x22＋x32＋x42＋x52=1x13＋x23＋x33＋x43＋x53=1x14＋x24＋x34＋x44＋x54=1endint20求解得到结果为：x14=x21=x32=x43=1，其它变量为0，成绩为253.2〃=4＇13〃2.即应当选派甲乙丙丁4人组成接力队，分别参加自由泳、蝶泳、仰泳、蛙泳的比赛。例3选课策略某学校规定，运筹学专业的学生毕业时必须至少学习过两门数学课，三门运筹学课和两门计算机课，这些课程的编号、名称、学分、所属类别和先修课要求如下表所示，毕业时学生最少可以学习这些课程中的哪些课程。课程编号课程名称学分所属类别先修课要求1微积分5数学132线性代数4数学3最优化方法4数学；运筹学微积分；线性代数4数据结构3数学；计算机计算机编程5应用统计4数学；运筹学微积分；线性代数6计算机模拟3计算机；运筹学计算机编程7计算机编程2计算机8预测理论2运筹学应用统计9数学实验3运筹学；计算机微积分；线性代数模型建立用xi=1表示选修表中按编号顺序的9门课程（xi=0表示不选；i=1，2…，9）问题的目标为选修的课程总数最少，即MinZ=xi约束条件包括两个方面：第一，每人最少要学习2门数学课、3门运筹学课和2门计算机课，根据表中对每门课程所属类别的划分，这一约束可以表示为x1＋x2＋x3＋x4＋x5≥2x3＋x5＋x6＋x8＋x9≥3x4＋x6＋x7＋x9≥2第二，某些课程有先修课程的要求，例如“数据结构”的先修课是“计算机编程”，这意味着如果x4=1，必须x7=1，这个条件可以表示为x4≤x7（注意：x4=0时对x7没有限制）。“最优化方法”的先修课是“微积分”和“线性代数”的条件可表为x3≤x1，x3≤x2，而这两个不等式可以用一个约束表示为2x3-x1-x2≤0，14这样，所有课程的先修课要求可表为如下的约束2x3－x1－x2≤0x4－x7≤02x5―x1―x2≤0x6－x7≤0x8－x5≤02x9―x1―x2≤0模型求解将0-1规划模型输入LINDO，求解得到结果为x1=x2=x3=x6=x7=x9=1，其它变量0，对照课程编号，它们是微积分、线性代数，最优化方法、计算机模拟、计算机编程、数学实验，共6门课程，总学分为21。例4钢管下料问题某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出，从钢管厂进货时得到的原料钢管都是19m。现有一客户需要50根4m、20根6m和15根8m的钢管，应如何下料最节省？问题分析首先，应当确定哪些切割模式是可行的，所谓一个切割模式，是指按照客户需要在原料钢管上安排切割的一种组合，例如：我们可以将19m的钢管切割成3根4m的钢管，余料为7m；或者将19m的钢管切割成4m、6m和8m的钢管各1根，余料为1m，显然，可行的切割模式是很多的。其次，应当确定哪些切割模式是合理的，通常假设一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸，例如：将19m的钢管切割成3根4m的钢管是可行的，但余料为7m，可以进一步将7m的余料切割成4m钢管（余料为3m），或者将7m的余料切割成6m钢管（余料为1m）在这种15合理性假设下，切割模式一共有7种，如下表所示。4m钢管根数6m钢管根数8m钢管根数余料(m)模式14003模式23101模式32013模式41203模式51111模式60301模式70023问题化为在满足客户需要的条件下，按照哪些种合理的模式，切割多少根原料钢管，最为节省，而所谓节省，可以有两种标准：一是切割后剩余的总余料量最小，二是切割原料钢管的总根数最少，下面将对这两个目标分别讨论。模型建立用xi表示按照第i种模式（i=1，2，…，7）切割的原料钢管的根数，显然它们应当是非负整数。以切割后剩余的总余料量最小为目标，则由上表可得MinZ1=3x1＋x2＋3x3＋3x4＋x5＋x6＋3x7(1)以切割原料钢管的总根数量少为目标，则有MinZ2=x1＋x2＋x3＋x4＋x5＋x6＋x7(2)下面分别在这两种目标下求解。为满足客户的需求，按照上表应有164x1＋3x2＋2x3＋x4＋x5≥50(3)x2＋2x4＋x5＋3x6≥20(4)x3＋x5＋2x7≥15(5)模型求解1.将（1），（3），（4），（5）构成的整数线性规划模型（加上整数约束）输入LINDO如下：Min3x1＋x2＋3x3＋3x4＋x5＋x6＋3x7s.t4x1＋3x2＋2x3＋x4＋x5＞=50x2＋2x4＋x5＋3x6＞=20x3＋x5＋2x7＞=15endgin7求解可以得到最优解如下：OBJECTIVEFUNCTIONVALUE1）27.00000VARIABLEVALUEREDUCEDCOSTX10.0000003.000000X212.0000001.000000X30.0000003.000000X40.0000003.000000X515.0000001.000000X60.0000001.000000X70.0000003.000000即按照模式2切割12根原料钢管，按照模式5切割15根原料钢管，共27根，总余料量为27m，显然，在总余料量最小的目标下，最优解将是使用余料尽可能小的切割模式（模式2和5的余料为1m），这会导致切割原料钢管的总根数较多。172、将(2)～(5)构成的整数线性规划模型（加上整数约束）输入LINDO求解，可以得到最优解如下：OBJECTIVEFUNCTIONVALUE1）25.00000VARIABLEVALUEREDUCEDCOSTX10.0000001.000000X215.0000001.000000X30.0000001.000000X40.0000001.000000X55.0000001.000000X60.0000001.000000X75.0000001.000000即按照模式2切割15根原料钢管，按模式5切割5根、按模式7切割5根、共25根，可算出总余料量为35m，与上面得到的结果相比，总余料量增加了8m，但是所用的原料钢管的总根数减少了2根，在余料没有什么用途的情况下，通常选择总根数量少为目标。18',)