2023年中考数学复习最新真题源专题讲义专题讲义(四)-图形的认识

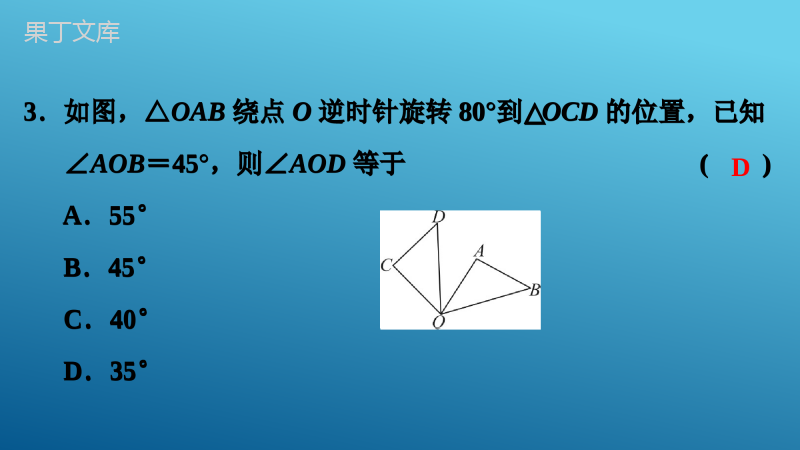
专题讲义(四)图形的认识专题讲义(四)图形的认识一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列图形既是轴对称图形，又是中心对称图形的是()D一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列图形既是轴对称图形，又是中心对称图形的是()2．作一个角等于已知角，其尺规作图的原理是()A．SSSB．SASC．AASD．ASAA2．作一个角等于已知角，其尺规作图的原理是()A．SSSB．SASC．AASD．ASA3．如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB＝45°，则∠AOD等于()A．55°B．45°C．40°D．35°D3．如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB＝45°，则∠AOD等于()A．55°B．45°C．40°D．35°4．如图所示的几何体是由一个圆锥和一个长方体组成的，则它的俯视图是()A4．如图所示的几何体是由一个圆锥和一个长方体组成的，则它的俯视图是()5．(2022·宿迁)下列展开图中，是正方体展开图的是()C5．(2022·宿迁)下列展开图中，是正方体展开图的是()6.如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是()A．仅主视图不同B．仅俯视图不同C．仅左视图不同D．主视图、左视图和俯视图都相同D6.如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是()A．仅主视图不同B．仅俯视图不同C．仅左视图不同D．主视图、左视图和俯视图都相同7．下列图形中，表示两棵小树在同一时刻阳光下的影子的图形可能是()A7．下列图形中，表示两棵小树在同一时刻阳光下的影子的图形可能是()8．如图，将边长为4的菱形ABCD纸片折叠，使点A恰好落在对角线的交点O处，若折痕EF＝23，则∠A＝()A．120°B．100°C．60°D．30°A8．如图，将边长为4的菱形ABCD纸片折叠，使点A恰好落在对角线的交点O处，若折痕EF＝23，则∠A＝()A．120°B．100°C．60°D．30°9．已知直线m∥n，将一块含45°角的直角三角板ABC按如图位置放置，其中斜边BC与直线n相交于点D，若∠1＝25°，则∠2的度数为()A．60°B．65°C．70°D．75°C9．已知直线m∥n，将一块含45°角的直角三角板ABC按如图位置放置，其中斜边BC与直线n相交于点D，若∠1＝25°，则∠2的度数为()A．60°B．65°C．70°D．75°10．如图，AC＝AD，BC＝BD，则()A．CD垂直平分ABB．AB垂直平分CDC．CD平分∠ACBD．以上结论都不正确B10．如图，AC＝AD，BC＝BD，则()A．CD垂直平分ABB．AB垂直平分CDC．CD平分∠ACBD．以上结论都不正确二、填空题：本大题共5小题，每小题3分，共15分．11．已知∠A＝65°，则∠A的补角等于_____.12．正八边形的每个外角的度数为_____.13．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C＝48°，则∠AED为_____°.115°45°114二、填空题：本大题共5小题，每小题3分，共15分．11．已知∠A＝65°，则∠A的补角等于_____.12．正八边形的每个外角的度数为_____.13．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C＝48°，则∠AED为_____°.14．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，则点C到AB的距离是_____.15．已知点C在线段AB上，线段AC＝7cm，BC＝5cm，点M，N分别是AC，BC的中点，则MN的长度为____cm.4.8614．如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，则点C到AB的距离是_____.15．已知点C在线段AB上，线段AC＝7cm，BC＝5cm，点M，N分别是AC，BC的中点，则MN的长度为____cm.三、解答题(一)：本大题共3小题，每小题8分，共24分．16．如图，直线AB，CD相交于O，∠AOC＝28°，OE平分∠AOD，求∠EOC的度数．三、解答题(一)：本大题共3小题，每小题8分，共24分．16．如图，直线AB，CD相交于O，∠AOC＝28°，OE平分∠AOD，求∠EOC的度数．解：∵OE平分∠AOD，∴∠AOE＝∠EOD＝12∠AOD，又∵∠AOC＝28°，∠AOD＋∠AOC＝180°，∴∠AOD＝152°，∴∠AOE＝76°，∴∠EOC＝∠AOC＋∠AOE＝28°＋76°＝104°.解：∵OE平分∠AOD，∴∠AOE＝∠EOD＝12∠AOD，又∵∠AOC＝28°，∠AOD＋∠AOC＝180°，∴∠AOD＝152°，∴∠AOE＝76°，∴∠EOC＝∠AOC＋∠AOE＝28°＋76°＝104°.17．如图，AB∥CD，点E是CD上一点，∠AEC＝42°，EF平分∠AED交AB于点F，求∠AFE的度数．17．如图，AB∥CD，点E是CD上一点，∠AEC＝42°，EF平分∠AED交AB于点F，求∠AFE的度数．解：∵∠AEC＝42°，∴∠AED＝180°－∠AEC＝138°，∵EF平分∠AED，∴∠DEF＝12∠AED＝69°，又∵AB∥CD，∴∠AFE＝∠DEF＝69°.解：∵∠AEC＝42°，∴∠AED＝180°－∠AEC＝138°，∵EF平分∠AED，∴∠DEF＝12∠AED＝69°，又∵AB∥CD，∴∠AFE＝∠DEF＝69°.18．5个棱长为1的正方体组成如图所示的几何体，画出该几何体从正面看和从左面看的平面图形．18．5个棱长为1的正方体组成如图所示的几何体，画出该几何体从正面看和从左面看的平面图形．解：所画图形如下所示：(从正面看)(从左面看)解：所画图形如下所示：(从正面看)(从左面看)四、解答题(二)：本大题共3小题，每小题9分，共27分．19．如图，在直线MN的异侧有A，B两点，按要求画图取点，并写出画图的依据．(1)在直线MN上取一点C，使线段AC最短．依据是_____________；(2)在直线MN上取一点D，使线段AD＋BD最短．依据是____________________．垂线段最短两点之间，线段最短四、解答题(二)：本大题共3小题，每小题9分，共27分．19．如图，在直线MN的异侧有A，B两点，按要求画图取点，并写出画图的依据．(1)在直线MN上取一点C，使线段AC最短．依据是_____________；(2)在直线MN上取一点D，使线段AD＋BD最短．依据是____________________．解：(1)如图，过A作AC⊥MN，依据：垂线段最短，故答案为垂线段最短．解：(2)如图，连接AB交MN于D，依据：两点之间，线段最短，故答案为两点之间，线段最短．解：(1)如图，过A作AC⊥MN，依据：垂线段最短，故答案为垂线段最短．解：(2)如图，连接AB交MN于D，依据：两点之间，线段最短，故答案为两点之间，线段最短．20．如图，在△ABC中，∠A＝90°，BD平分∠ABC，AC＝8cm，AB＝6cm，求点D到直线BC的距离．20．如图，在△ABC中，∠A＝90°，BD平分∠ABC，AC＝8cm，AB＝6cm，求点D到直线BC的距离．解：如图，过点D作DE⊥BC于点E，∵∠A＝∠BED＝90°，BD平分∠ABC，∴AD＝ED，∴Rt△ABD≌Rt△EBD.∴AB＝BE.∵BC＝AB2＋AC2＝62＋82＝10(cm)设DE＝x，则AD＝x,∴CD＝8－x，又EC＝10－BE＝10－AB＝10－6＝4(cm)．∵在Rt△DEC中，由勾股定理，得CD2＝EC2＋DE2即(8－x)2＝42＋x2，解得x＝3，∴DE＝3cm，即点D到直线BC的距离是3cm.解：如图，过点D作DE⊥BC于点E，∵∠A＝∠BED＝90°，BD平分∠ABC，∴AD＝ED，∴Rt△ABD≌Rt△EBD.∴AB＝BE.∵BC＝AB2＋AC2＝62＋82＝10(cm)设DE＝x，则AD＝x,∴CD＝8－x，又EC＝10－BE＝10－AB＝10－6＝4(cm)．∵在Rt△DEC中，由勾股定理，得CD2＝EC2＋DE2即(8－x)2＝42＋x2，解得x＝3，∴DE＝3cm，即点D到直线BC的距离是3cm.21．如图，在平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(－3，4)，B(－5，2)，C(－2，1)．21．如图，在平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(－3，4)，B(－5，2)，C(－2，1)．(1)画出△ABC关于y轴对称的图形△A1B1C1；(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2；(3)求(2)中线段OA扫过的图形的面积．(1)画出△ABC关于y轴对称的图形△A1B1C1；(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2；(3)求(2)中线段OA扫过的图形的面积．解：(1)如图，△A1B1C1即为所求；解：(2)如图，△A2B2C2即为所求；解：(3)∵OA＝32＋42＝5，∴线段OA扫过的图形面积＝90π×52360＝254π.解：(1)如图，△A1B1C1即为所求；解：(2)如图，△A2B2C2即为所求；解：(3)∵OA＝32＋42＝5，∴线段OA扫过的图形面积＝90π×52360＝254π.五、解答题(三)：本大题共2小题，每小题12分，共24分．22．如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF.(1)若∠AOE＝40°，求∠BOD的度数；(2)若∠AOE＝α，求∠BOD的度数．(用含α的代数式表示)五、解答题(三)：本大题共2小题，每小题12分，共24分．22．如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF.(1)若∠AOE＝40°，求∠BOD的度数；(2)若∠AOE＝α，求∠BOD的度数．(用含α的代数式表示)解：(1)∵∠AOE＋∠AOF＝180°(互为补角)，∠AOE＝40°，∴∠AOF＝140°.又∵OC平分∠AOF，∴∠FOC＝12∠AOF＝70°，∴∠EOD＝∠FOC＝70°(对顶角相等)．而∠BOE＝∠AOB－∠AOE＝50°，∴∠BOD＝∠EOD－∠BOE＝20°；解：(1)∵∠AOE＋∠AOF＝180°(互为补角)，∠AOE＝40°，∴∠AOF＝140°.又∵OC平分∠AOF，∴∠FOC＝12∠AOF＝70°，∴∠EOD＝∠FOC＝70°(对顶角相等)．而∠BOE＝∠AOB－∠AOE＝50°，∴∠BOD＝∠EOD－∠BOE＝20°；解：(2)∵∠AOE＋∠AOF＝180°(互为补角)，∠AOE＝α，∴∠AOF＝180°－α；又∵OC平分∠AOF，∴∠FOC＝12∠AOF＝90°－12α，∴∠EOD＝∠FOC＝90°－12α(对顶角相等)；而∠BOE＝∠AOB－∠AOE＝90°－α，∴∠BOD＝∠EOD－∠BOE＝12α.解：(2)∵∠AOE＋∠AOF＝180°(互为补角)，∠AOE＝α，∴∠AOF＝180°－α；又∵OC平分∠AOF，∴∠FOC＝12∠AOF＝90°－12α，∴∠EOD＝∠FOC＝90°－12α(对顶角相等)；而∠BOE＝∠AOB－∠AOE＝90°－α，∴∠BOD＝∠EOD－∠BOE＝12α.23．已知AB∥CD，点P是平面内一点．(1)如图1，若点P在AB，CD内部，请探究∠BPD，∠B，∠D之间有何数量关系？请证明你的结论；(2)如图2，若点P移动到AB，CD外部，那么∠BPD，∠B，∠D之间的数量关系是否发生变化？请给出你的证明．23．已知AB∥CD，点P是平面内一点．(1)如图1，若点P在AB，CD内部，请探究∠BPD，∠B，∠D之间有何数量关系？请证明你的结论；(2)如图2，若点P移动到AB，CD外部，那么∠BPD，∠B，∠D之间的数量关系是否发生变化？请给出你的证明．解：(1)∠BPD＝∠B＋∠D，证明如下：作PQ∥AB，如图，∵AB∥CD，∴AB∥PQ∥CD，∴∠1＝∠B，∠2＝∠D，∴∠BPD＝∠B＋∠D.解：(1)∠BPD＝∠B＋∠D，证明如下：作PQ∥AB，如图，∵AB∥CD，∴AB∥PQ∥CD，∴∠1＝∠B，∠2＝∠D，∴∠BPD＝∠B＋∠D.解：(2)发生变化，应该为∠BPD＝∠B－∠D，证明如下：∵AB∥CD，∴∠B＝∠BOD，而∠BOD＝∠BPD＋∠D，∴∠B＝∠BPD＋∠D，∴∠BPD＝∠B－∠D.解：(2)发生变化，应该为∠BPD＝∠B－∠D，证明如下：∵AB∥CD，∴∠B＝∠BOD，而∠BOD＝∠BPD＋∠D，∴∠B＝∠BPD＋∠D，∴∠BPD＝∠B－∠D.