2023年中考数学复习最新真题源专题讲义专题讲义(八)-圆

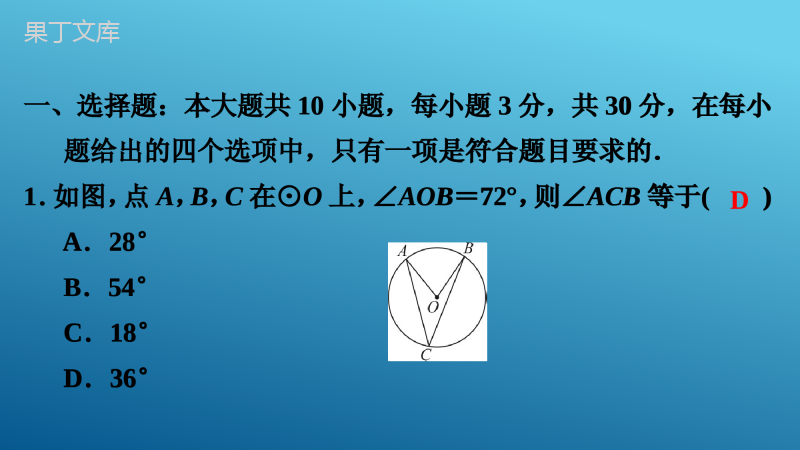
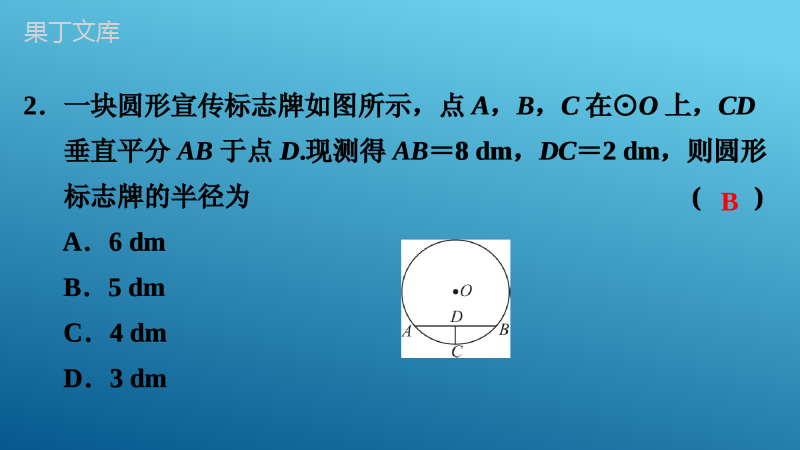
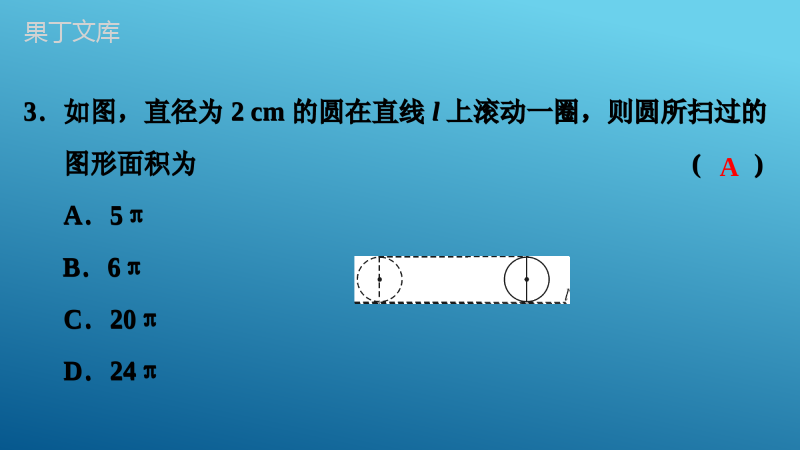
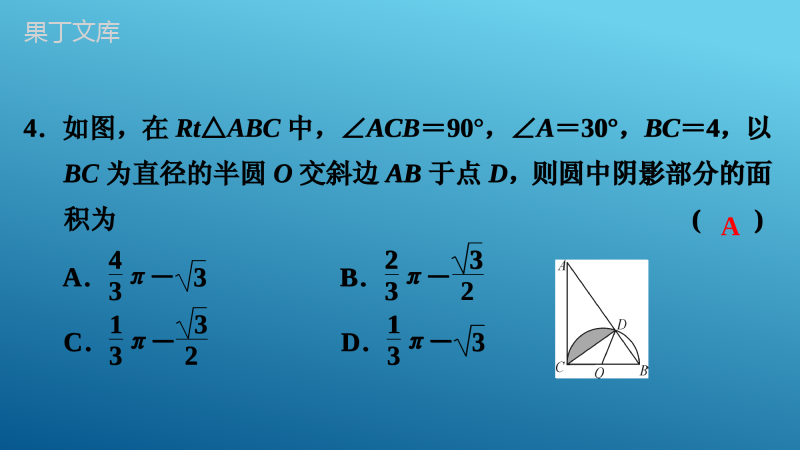
专题讲义(八)圆专题讲义(八)圆一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，点A，B，C在⊙O上，∠AOB＝72°，则∠ACB等于()A．28°B．54°C．18°D．36°D一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，点A，B，C在⊙O上，∠AOB＝72°，则∠ACB等于()A．28°B．54°C．18°D．36°2．一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D.现测得AB＝8dm，DC＝2dm，则圆形标志牌的半径为()A．6dmB．5dmC．4dmD．3dmB2．一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D.现测得AB＝8dm，DC＝2dm，则圆形标志牌的半径为()A．6dmB．5dmC．4dmD．3dm3．如图，直径为2cm的圆在直线l上滚动一圈，则圆所扫过的图形面积为()A．5πB．6πC．20πD．24πA3．如图，直径为2cm的圆在直线l上滚动一圈，则圆所扫过的图形面积为()A．5πB．6πC．20πD．24π4．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点D，则圆中阴影部分的面积为()A．43π－3B．23π－32C．13π－32D．13π－3A4．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点D，则圆中阴影部分的面积为()A．43π－3B．23π－32C．13π－32D．13π－35．下列说法正确的是()A．长度相等的弧叫等弧B．平分弦的直径一定垂直于该弦C．三角形的外心是三条角平分线的交点D．不在同一直线上的三个点确定一个圆D5．下列说法正确的是()A．长度相等的弧叫等弧B．平分弦的直径一定垂直于该弦C．三角形的外心是三条角平分线的交点D．不在同一直线上的三个点确定一个圆6．如图，⊙O的直径AB＝6，若∠BAC＝50°，则劣弧AC的长为()A．2πB．8π3C．3π4D．4π3D6．如图，⊙O的直径AB＝6，若∠BAC＝50°，则劣弧AC的长为()A．2πB．8π3C．3π4D．4π37．如图，BD是⊙O的直径，点A，C在⊙O上，AB︵＝AD︵，AC交BD于点G，若∠COD＝126°，则∠AGB的度数为()A．99°B．108°C．110°D．117°B7．如图，BD是⊙O的直径，点A，C在⊙O上，AB︵＝AD︵，AC交BD于点G，若∠COD＝126°，则∠AGB的度数为()A．99°B．108°C．110°D．117°8．如图，△ABC是⊙O的内接三角形，AB＝BC，∠BAC＝30°，AD是直径，AD＝8，则AC的长为()A．4B．43C．833D．23B8．如图，△ABC是⊙O的内接三角形，AB＝BC，∠BAC＝30°，AD是直径，AD＝8，则AC的长为()A．4B．43C．833D．239．如图，四边形ABCD为⊙O的内接四边形，∠BCD＝120°，则∠BOD的大小是()A．80°B．120°C．100°D．90°B9．如图，四边形ABCD为⊙O的内接四边形，∠BCD＝120°，则∠BOD的大小是()A．80°B．120°C．100°D．90°10．如图，直径为10的⊙A经过点C和点O，点B是y轴右侧⊙A优弧上一点，∠OBC＝30°，则点C的坐标为()A．(0，5)B．(0，53)C．(0，523)D．(0，533)A10．如图，直径为10的⊙A经过点C和点O，点B是y轴右侧⊙A优弧上一点，∠OBC＝30°，则点C的坐标为()A．(0，5)B．(0，53)C．(0，523)D．(0，533)二、填空题：本大题共5小题，每小题3分，共15分．11．如图，△ABC为⊙O的内接三角形，AB是直径，∠A＝20°，则∠B＝____度．70二、填空题：本大题共5小题，每小题3分，共15分．11．如图，△ABC为⊙O的内接三角形，AB是直径，∠A＝20°，则∠B＝____度．12.(2021·温州)如图，⊙O与△OAB的边AB相切，切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B，边A′B交线段AO于点C.若∠A′＝25°，则∠OCB＝____度．13．(2022·宿迁)用半径为6cm，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆的半径是____cm.85212.(2021·温州)如图，⊙O与△OAB的边AB相切，切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B，边A′B交线段AO于点C.若∠A′＝25°，则∠OCB＝____度．13．(2022·宿迁)用半径为6cm，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆的半径是____cm.14．如图，PA，PB分别是⊙O的切线，A，B为切点，AC是⊙O的直径，已知∠BAC＝35°，则∠P的度数为_____.70°14．如图，PA，PB分别是⊙O的切线，A，B为切点，AC是⊙O的直径，已知∠BAC＝35°，则∠P的度数为_____.15．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r＝5，AC＝53，则cos∠B＝____.1215．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r＝5，AC＝53，则cos∠B＝____.12三、解答题(一)：本大题共3小题，每小题8分，共24分．16．如图，在⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD，BC.求证：(1)AD︵＝BC︵；(2)AE＝CE.三、解答题(一)：本大题共3小题，每小题8分，共24分．16．如图，在⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD，BC.求证：(1)AD︵＝BC︵；(2)AE＝CE.证明：(1)∵AB＝CD，∴AB︵＝CD︵，即AD︵＋AC︵＝BC︵＋AC︵，∴AD︵＝BC︵；证明：(2)∵AD︵＝BC︵，∴AD＝BC，又∵∠ADE＝∠CBE，∠DAE＝∠BCE，∴△ADE≌△CBE(ASA)，∴AE＝CE.证明：(1)∵AB＝CD，∴AB︵＝CD︵，即AD︵＋AC︵＝BC︵＋AC︵，∴AD︵＝BC︵；证明：(2)∵AD︵＝BC︵，∴AD＝BC，又∵∠ADE＝∠CBE，∠DAE＝∠BCE，∴△ADE≌△CBE(ASA)，∴AE＝CE.17．如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°.(1)求∠BAC的度数；(2)若PA＝1，求点O到弦AB的距离．17．如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°.(1)求∠BAC的度数；(2)若PA＝1，求点O到弦AB的距离．解：(1)∵PA切⊙O于点A，PB切⊙O于点B，∴PA＝PB，∠PAC＝90°，∵∠APB＝60°，∴△APB是等边三角形，∴∠BAP＝60°，∴∠BAC＝90°－∠BAP＝30°.解：(1)∵PA切⊙O于点A，PB切⊙O于点B，∴PA＝PB，∠PAC＝90°，∵∠APB＝60°，∴△APB是等边三角形，∴∠BAP＝60°，∴∠BAC＝90°－∠BAP＝30°.解：(2)作OD⊥AB于D，如图所示：则AD＝BD＝12AB，由(1)得△APB是等边三角形，∴AB＝PA＝1，∴AD＝12，∵∠BAC＝30°，∴OD＝33AD＝33×12＝36，即点O到弦AB的距离为36.解：(2)作OD⊥AB于D，如图所示：则AD＝BD＝12AB，由(1)得△APB是等边三角形，∴AB＝PA＝1，∴AD＝12，∵∠BAC＝30°，∴OD＝33AD＝33×12＝36，即点O到弦AB的距离为36.18．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点)．将△ABC绕点B顺时针旋转90°得到△A′BC′，画出△A′BC′，并求BA边旋转到BA′位置时所扫过图形的面积．18．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点)．将△ABC绕点B顺时针旋转90°得到△A′BC′，画出△A′BC′，并求BA边旋转到BA′位置时所扫过图形的面积．解：如图：∵AB＝32＋22＝13，∴BA边旋转到BA′位置时所扫过图形的面积为：90π×（13）2360＝13π4.解：如图：∵AB＝32＋22＝13，∴BA边旋转到BA′位置时所扫过图形的面积为：90π×（13）2360＝13π4.四、解答题(二)：本大题共3小题，每小题9分，共27分．19．(2022·邵阳)如图，已知DC是⊙O的直径，点B为CD延长线上一点，AB是⊙O的切线，点A为切点，且AB＝AC.(1)求∠ACB的度数；(2)若⊙O的半径为3，求圆弧AC︵的长．四、解答题(二)：本大题共3小题，每小题9分，共27分．19．(2022·邵阳)如图，已知DC是⊙O的直径，点B为CD延长线上一点，AB是⊙O的切线，点A为切点，且AB＝AC.(1)求∠ACB的度数；(2)若⊙O的半径为3，求圆弧AC︵的长．解：(1)如图，连接OA，∵AB是⊙O的切线，点A为切点，∴∠BAO＝90°，又∵AB＝AC，OA＝OC，∴∠B＝∠ACB＝∠OAC，设∠ACB＝x°，则在△ABC中，x°＋x°＋x°＋90°＝180°，解得：x＝30，∴∠ACB的度数为30°；解：(1)如图，连接OA，∵AB是⊙O的切线，点A为切点，∴∠BAO＝90°，又∵AB＝AC，OA＝OC，∴∠B＝∠ACB＝∠OAC，设∠ACB＝x°，则在△ABC中，x°＋x°＋x°＋90°＝180°，解得：x＝30，∴∠ACB的度数为30°；解：(2)∵∠ACB＝∠OAC＝30°，∴∠AOC＝120°，∴lAC︵＝120π×3180＝2π.解：(2)∵∠ACB＝∠OAC＝30°，∴∠AOC＝120°，∴lAC︵＝120π×3180＝2π.20．如图，AB为⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD.(1)求证：PD是⊙O的切线；(2)当四边形POBD是平行四边形时，求∠APO的度数．20．如图，AB为⊙O的直径，过点A作⊙O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD∥OP，交⊙O于点D，连接PD.(1)求证：PD是⊙O的切线；(2)当四边形POBD是平行四边形时，求∠APO的度数．(1)证明：连接OD，∵PA切⊙O于A，∴PA⊥AB，即∠PAO＝90°，∵OP∥BD，∴∠DBO＝∠AOP，∠BDO＝∠DOP，∵OD＝OB，∴∠BDO＝∠DBO，∴∠DOP＝∠AOP，在△AOP和△DOP中，AO＝DO，∠AOP＝∠DOP，PO＝PO，∴△AOP≌△DOP(SAS)，∴∠PDO＝∠PAO，∵∠PAO＝90°，∴∠PDO＝90°，即OD丄PD，∵OD过点O，∴PD是⊙O的切线；(1)证明：连接OD，∵PA切⊙O于A，∴PA⊥AB，即∠PAO＝90°，∵OP∥BD，∴∠DBO＝∠AOP，∠BDO＝∠DOP，∵OD＝OB，∴∠BDO＝∠DBO，∴∠DOP＝∠AOP，在△AOP和△DOP中，AO＝DO，∠AOP＝∠DOP，PO＝PO，∴△AOP≌△DOP(SAS)，∴∠PDO＝∠PAO，∵∠PAO＝90°，∴∠PDO＝90°，即OD丄PD，∵OD过点O，∴PD是⊙O的切线；(2)解：由(1)知：△AOP≌△DOP，∴PA＝PD，∵四边形POBD是平行四边形，∴PD＝OB，∵OB＝OA，∴PA＝OA，∴∠APO＝∠AOP，∵∠PAO＝90°，∴∠APO＝∠AOP＝45°.(2)解：由(1)知：△AOP≌△DOP，∴PA＝PD，∵四边形POBD是平行四边形，∴PD＝OB，∵OB＝OA，∴PA＝OA，∴∠APO＝∠AOP，∵∠PAO＝90°，∴∠APO＝∠AOP＝45°.21．(2022·河池)如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D.且∠PCA＝∠CBD.(1)求证：PC为⊙O的切线；(2)若PC＝22BO，PB＝12，求⊙O的半径及BE的长．21．(2022·河池)如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D.且∠PCA＝∠CBD.(1)求证：PC为⊙O的切线；(2)若PC＝22BO，PB＝12，求⊙O的半径及BE的长．(1)证明：如图，连接OC，∵BC平分∠ABE，∴∠ABC＝∠CBD，∵OC＝OB，∴∠ABC＝∠OCB，∵∠PCA＝∠CBD，∴∠PCA＝∠OCB，∵AB是直径，∴∠ACB＝90°，∴∠ACO＋∠OCB＝90°，∴∠PCA＋∠ACO＝90°，∴∠PCO＝90°，∴OC丄PC，∵OC是半径，∴PC是⊙O的切线；(1)证明：如图，连接OC，∵BC平分∠ABE，∴∠ABC＝∠CBD，∵OC＝OB，∴∠ABC＝∠OCB，∵∠PCA＝∠CBD，∴∠PCA＝∠OCB，∵AB是直径，∴∠ACB＝90°，∴∠ACO＋∠OCB＝90°，∴∠PCA＋∠ACO＝90°，∴∠PCO＝90°，∴OC丄PC，∵OC是半径，∴PC是⊙O的切线；(2)解：如图，连接AE，设OB＝OC＝r，∵PC＝22OB，∴PC＝22r，∴OP＝OC2＋PC2＝r2＋（22r）2＝3r，∵PB＝12，∴4r＝12，∴r＝3，由(1)可知，∠OCB＝∠CBD，∴OC∥BD，∴OCBD＝OPPB，∠D＝∠PCO＝90°，∴3BD＝912，∴BD＝4，∵AB是直径，∴∠AEB＝90°，∴∠AEB＝∠D＝90°，∴AE∥PD，∴BEBD＝BABP，∴BE4＝912，∴BE＝3.(2)解：如图，连接AE，设OB＝OC＝r，∵PC＝22OB，∴PC＝22r，∴OP＝OC2＋PC2＝r2＋（22r）2＝3r，∵PB＝12，∴4r＝12，∴r＝3，由(1)可知，∠OCB＝∠CBD，∴OC∥BD，∴OCBD＝OPPB，∠D＝∠PCO＝90°，∴3BD＝912，∴BD＝4，∵AB是直径，∴∠AEB＝90°，∴∠AEB＝∠D＝90°，∴AE∥PD，∴BEBD＝BABP，∴BE4＝912，∴BE＝3.五、解答题(三)：本大题共2小题，每小题12分，共24分．22．(2020·上海)如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D.(1)求证：∠BAC＝2∠ABD；(2)当△BCD是等腰三角形时，求∠BCD的大小；(3)当AD＝2，CD＝3时，求边BC的长．五、解答题(三)：本大题共2小题，每小题12分，共24分．22．(2020·上海)如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D.(1)求证：∠BAC＝2∠ABD；(2)当△BCD是等腰三角形时，求∠BCD的大小；(3)当AD＝2，CD＝3时，求边BC的长．(1)证明：如图，连接OA，OC，∵AB＝AC，OA＝OA，OB＝OC，∴△AOB≌△AOC(SSS)，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠ABD；(1)证明：如图，连接OA，OC，∵AB＝AC，OA＝OA，OB＝OC，∴△AOB≌△AOC(SSS)，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠ABD；(2)解：①若BD＝CB，则∠BCD＝∠BDC＝∠ABD＋∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC＋∠C＋∠BDC＝180°，∴8∠ABD＝180°，∴∠ABD＝22.5°，∴∠BCD＝3∠ABD＝67.5°.②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠BCD＝4∠ABD，∵∠DBC＋∠BCD＋∠CDB＝180°，∴10∠ABD＝180°，∴∠ABD＝18°，∴∠BCD＝4∠ABD＝72°.③若DB＝DC，则D与A重合，这种情形不存在．综上所述，∠BCD的值为67.5°或72°；(2)解：①若BD＝CB，则∠BCD＝∠BDC＝∠ABD＋∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC＋∠C＋∠BDC＝180°，∴8∠ABD＝180°，∴∠ABD＝22.5°，∴∠BCD＝3∠ABD＝67.5°.②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠BCD＝4∠ABD，∵∠DBC＋∠BCD＋∠CDB＝180°，∴10∠ABD＝180°，∴∠ABD＝18°，∴∠BCD＝4∠ABD＝72°.③若DB＝DC，则D与A重合，这种情形不存在．综上所述，∠BCD的值为67.5°或72°；(3)解：如图1，延长AO交BC于点H，∵AB＝AC，∠BAH＝∠CAH，∴AH⊥BC，∴BH＝12BC.作AE∥BC交BD的延长线于点E.则AEBC＝ADDC＝23，∴AOOH＝AEBH＝43，设OB＝OA＝4a，OH＝3a，∵AB2－AH2＝OB2－OH2，AB＝AC＝5，∴25－49a2＝16a2－9a2，∴a2＝2556，∴BH＝OB2－OH2＝7a2＝524，∴BC＝2BH＝522.(3)解：如图1，延长AO交BC于点H，∵AB＝AC，∠BAH＝∠CAH，∴AH⊥BC，∴BH＝12BC.作AE∥BC交BD的延长线于点E.则AEBC＝ADDC＝23，∴AOOH＝AEBH＝43，设OB＝OA＝4a，OH＝3a，∵AB2－AH2＝OB2－OH2，AB＝AC＝5，∴25－49a2＝16a2－9a2，∴a2＝2556，∴BH＝OB2－OH2＝7a2＝524，∴BC＝2BH＝522.23．(2020·临沂)已知⊙O1的半径为r1，⊙O2的半径为r2.以O1为圆心，以r1＋r2的长为半径画弧，再以线段O1O2的中点P为圆心，以12O1O2的长为半径画弧，两弧交于点A，连接O1A，O2A，O1A交⊙O1于点B，过点B作O2A的平行线BC交O1O2于点C.(1)求证：BC是⊙O2的切线；(2)若r1＝2，r2＝1，O1O2＝6，求阴影部分的面积．23．(2020·临沂)已知⊙O1的半径为r1，⊙O2的半径为r2.以O1为圆心，以r1＋r2的长为半径画弧，再以线段O1O2的中点P为圆心，以12O1O2的长为半径画弧，两弧交于点A，连接O1A，O2A，O1A交⊙O1于点B，过点B作O2A的平行线BC交O1O2于点C.(1)求证：BC是⊙O2的切线；(2)若r1＝2，r2＝1，O1O2＝6，求阴影部分的面积．(1)证明：如图，连接AP，O1O2交⊙O1于点E.∵以线段O1O2的中点P为圆心，以12O1O2的长为半径画弧，∴O1P＝AP＝O2P＝12O1O2，∴∠O1AO2＝90°，∵BC∥O2A，∴∠O1BC＝∠O1AO2＝90°，如图，过点O2作O2D⊥BC交BC的延长线于点D，∴四边形ABDO2是矩形，∴AB＝O2D，∵O1A＝r1＋r2，∴O2D＝r2，∴BC是⊙O2的切线；(1)证明：如图，连接AP，O1O2交⊙O1于点E.∵以线段O1O2的中点P为圆心，以12O1O2的长为半径画弧，∴O1P＝AP＝O2P＝12O1O2，∴∠O1AO2＝90°，∵BC∥O2A，∴∠O1BC＝∠O1AO2＝90°，如图，过点O2作O2D⊥BC交BC的延长线于点D，∴四边形ABDO2是矩形，∴AB＝O2D，∵O1A＝r1＋r2，∴O2D＝r2，∴BC是⊙O2的切线；(2)解：∵r1＝2，r2＝1，O1O2＝6，∴O1A＝12O1O2＝3，∴∠BO1C＝60°，∴O1C＝2O1B＝4，∴BC＝O1C2－O1B2＝42－22＝23，∴S阴影＝S△O1BC－S扇形BO1E＝12O1B·BC－60π×r21360＝12×2×23－60×π×22360＝23－23π.(2)解：∵r1＝2，r2＝1，O1O2＝6，∴O1A＝12O1O2＝3，∴∠BO1C＝60°，∴O1C＝2O1B＝4，∴BC＝O1C2－O1B2＝42－22＝23，∴S阴影＝S△O1BC－S扇形BO1E＝12O1B·BC－60π×r21360＝12×2×23－60×π×22360＝23－23π.