人教版九年级上册数学第22章二次函数y=a(x-h)2+k的图象和性质-第3课时

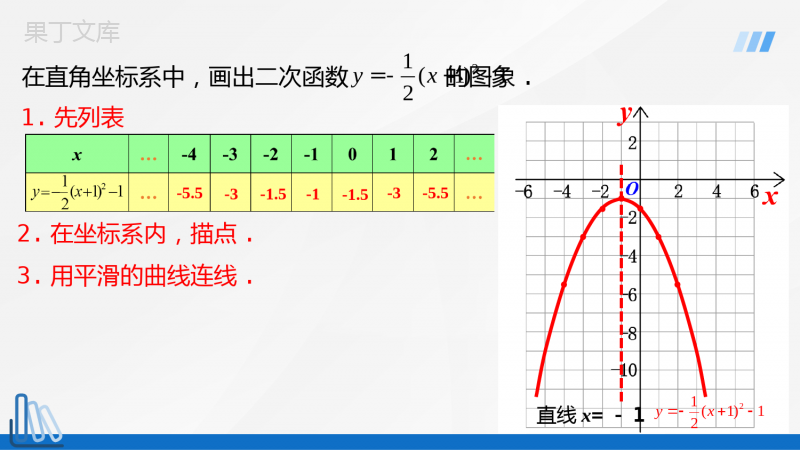
人教版数学九年级上册时间：22.1.3二次函数y=a(x-h)2+k的图象和性质11/13/2023第3课时学习目标素养目标（1）会用描点法画二次函数y=a(x-h)2+k的图象.（2）能说出抛物线y=a(x-h)2+k与抛物线y=ax2的相互关系.（3）能说出抛物线y=a(x-h)2+k的开口方向、对称轴、顶点.复习回顾二次函数y=a(x-h)2（a≠0）的性质a＞0a＜0图象开口方向对称轴顶点坐标最值增减性h>0h>0复习回顾抛物线y=ax2+k怎样由抛物线y=ax2平移得到？抛物线y=a(x-h)2怎样由抛物线y=ax2平移得到？向左平移h个单位向右平移h个单位口决：左加右减2+0yaxhh（＞）20yaxhh（＞）2yax2yaxy=ax2向上平移k个单位y=ax2+k(k＞0)y=ax2向下平移k个单位y=ax2-k(k＞0)口决：上加下减猜想：抛物线y=a(x-h)2+k怎样由抛物线y=ax2平移得到？在直角坐标系中，画出二次函数的图象.21(1)12yx=-+-1.先列表-5.5-3-1.5-1-1.5-3-5.52.在坐标系内，描点.3.用平滑的曲线连线.21(1)12yx直线x=－121(1)12yx=-+-1.抛物线的开口方向、对称轴、顶点各是什么？抛物线的开口______、对称轴_________、顶点是_______.向下直线x=－121(1)12yx=-+-直线x=－1(-1,-1)2.抛物线的最值、增减性又如何？(1)顶点都是最____点，函数都有最____值，最____值为_______;(2)当x＞-1(对称轴右侧)时_______________，当x＜-1时(对称轴左侧)_______________.高大y=-1y随x增大而增大y随x增大而减小大21(1)12yx=-+-3.怎样移动抛物线就可以得到抛物线？平移方法1：21(1)12yx212yx212yx2112yx向下平移1个单位21(1)12yx向左平移1个单位平移方法2：212yx21+12yx向左平移1个单位21(1)12yx向下平移1个单位复习回顾y=a(x-h)2+k（a≠0）的图象与性质a＞0a＜0图象开口方向对称轴顶点坐标最值增减性一般地，抛物线y=a(x-h)2+k与y=ax2形状相同，位置不同.把抛物线y=ax2向上(下)向左(右)平移，可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h、k的值来决定.2yax向左(或右)平移h个单位2yaxh平移k个单位向上(或下)2yaxhk向左(或右)平移h个单位2yaxk平移k个单位向上(或下)y=a(x-h)2+k顶点式二次函数开口方向对称轴顶点坐标y=-2(x-3)2+5向下(-1,2)向下向下(4,5)(3,-4)向上直线x=3直线x=-1直线x=4直线x=3(3,5)y=-3(x+1)2+2y=4(x-4)2+5y=-2(3-x)2-4完成下列表格:要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长.例43解：如图,以水管与地面交点为原点，原点与水柱落地处所在直线为x轴，水管所在直线为y轴，建立直角坐标系.点(1,3)是图中这段抛物线的顶点，因此，可设这段抛物线对应的函数是y=a(x-1)²+3（0≤x≤3）由这段抛物线经过点(3,0)可得0=a(3-1)²+3，当x=0时，y=2.25，也就是说，水管应长2.25m.3yxx23(1)3(03)4=-因此a34解得说出下面函数的开口方向、对称轴和顶点.（1）y=2(x+3)2+5；（2）y=-3(x-1)2-2；（3）y=4(x-3)2+7；（4）y=-5(x+2)2-6.开口向上对称轴为x=-3顶点坐标为（-3，5）开口向下对称轴为x=1顶点坐标为（1，-2）开口向上对称轴为x=3顶点坐标为（3，7）开口向下对称轴为x=-2顶点坐标为（-2，-6）练习【教材P35练习】随堂演练1.对称轴是直线x=-2的抛物线是()A.y=-2x2-2B.y=-2x2＋2C.y=-(x+2)2-2D.y=-5(x-2)2-62.将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（）A.y=3(x-2)2-1B.y=3(x-2)2+1C.y=3(x+2)2-1D.y=3(x+2)2+13.若抛物线的顶点为(3,5),则此抛物线的解析式可设为()基础巩固CCB4.指出下面函数的开口方向，对称轴和顶点坐标.（1）y=5(x+2)2+1；（2）y=-7(x-2)2-1；（3）y=(x-4)2+3；（4）y=-(x+2)2-3.开口向上对称轴为x=-2顶点坐标为（-2，1）开口向下对称轴为x=2顶点坐标为（2，-1）开口向上对称轴为x=4顶点坐标为（4，3）开口向下对称轴为x=-2顶点坐标为（-2，-3）5.在同一坐标系内，画出函数y=(x+2)2-2和y=(x-1)2+2的图象，并写出它的对称轴、顶点和最值.解：图象如图.1212yxx21(2)222222-，-、（-，-）、-；对称轴为顶点为最小值为yxx.21(1)212122，、（，）、对称轴为顶点为最小值为综合应用6.已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式．解：由函数顶点坐标是（1，-2），设二次函数的关系式为y=a(x-1)2-2.图象过点(0，0)，则0=a(0-1)2-2，解得a=2∴这个二次函数的关系式为y=2(x-1)2-2.拓展延伸7.小敏在某次投篮中，球的运动线路是抛物线y=x2+3.5的一部分(如图)，若命中篮圈中心，则她与篮底的距离l是()A.3.5mB.4mC.4.5mD.4.6m15B课堂小结结合图象y=a(x-h)2+k（a≠0）的性质有哪些？