人教版九年级上册数学第21章一元二次方程

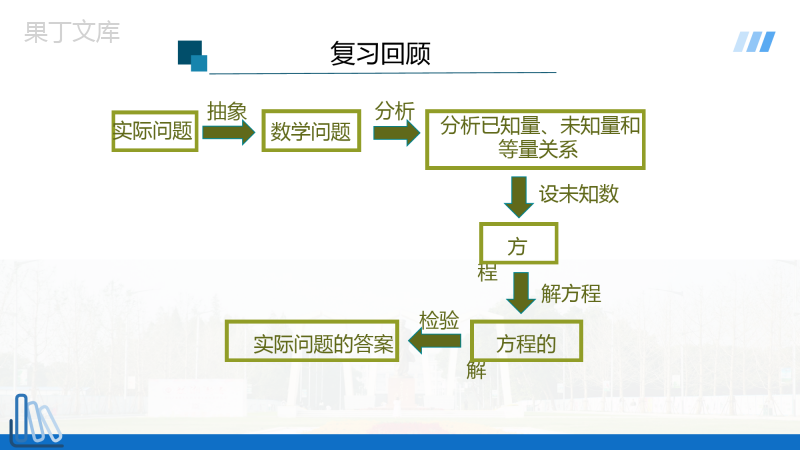
人教版数学九年级上册时间：21.1一元二次方程11/13/2023复习回顾一元一次方程：二元一次方程：分式方程：431x.325xy.31251.y复习回顾分析已知量、未知量和等量关系方程数学问题实际问题抽象分析设未知数方程的解检验实际问题的答案解方程知识回顾判断下列式子是否是一元一次方程：32x-3142x=一元一次方程1、只含有一个未知数2、未知数的次数都是13、等号两边都是整式2540xx+-=7154xy-=+3.理解一元二次方程解（根）的概念，并能解决相关问题.1.理解一元二次方程的概念，根据一元二次方程的一般形式，确定各项系数.2.灵活应用一元二次方程概念解决有关问题.素养目标课堂导入要设计一座2m高的人体雕像，使雕像的上部(腰以上)与下部(腰以下)的高度比，等于下部与全部的高度比，雕像的下部应设计为多高？ACB2mxm，即．解：雕像上部的高度AC，下部的高度BC应有如下关系：设雕像下部高xm，可得方程整理得x2+2x−4=0．x2=2(2−x)，2ACBCBC=2=2BCAC这个方程与我们学过的一元一次方程不同，x的最高次数是2．如何解这类方程？如何用这类方程解决一些实际问题？这就是本章我们要学习的内容．知识点1新知探究问题1如图，有一块矩形铁皮，长100cm，宽50cm，在它的四角各切一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm2，那么铁皮各角应切去多大的正方形？设切去的正方形的边长为xcm，则盒底的长为(100−2x)cm，宽为(50−2x)cm．根据方盒的底面积为3600cm2，得(100−2x)(50−2x)=3600．整理，得4x2−300x+1400=0．化简，得x2−75x+350=0．由上面的方程可以得出所切正方形的具体尺寸．解：知识点1新知探究问题2要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场．根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请多少个队参赛？由上面的方程可以得出参赛队数．全部比赛的场数为4×7=28．列方程x（x−1）=28，整理，得x²−x=28，化简，得x²−x=56．设应邀请x个队参赛，每个队要与其他(x−1)个队各赛一场，因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛，所以全部比赛共x（x−1）场．解：知识点1新知探究1．这些方程的两边都是整式；2．方程中只含有一个未知数，未知数的最高次数是2．x2−x=56x2−75x+350=0x2+2x−4=0观察由上面的问题得到的方程有什么特点？等号两边都是整式，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程，叫做一元二次方程．知识点2新知探究一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式：ax²+bx+c=0(a≠0)这种形式叫做一元二次方程的一般形式．其中ax2是二次项，a是二次项系数；bx是一次项，b是一次项系数；c是常数项．指出方程各项的系数时要带上前面的符号．一元二次方程ax2+bx+c=0(a≠0)中，为什么规定a≠0？b，c可以为0跟踪训练新知探究2．若方程(m+2)xm−3mx+1＝0是关于x的一元二次方程，则()A．m≠±2B．m＝2C．m＝−2D．m＝±21．下列方程，一元二次方程的个数是()①3x2+7=0；②x3+2x=1−x2+x3；③2x2−3y+1=0；④3x2−+6=0．A．1B．2C．3D．4BB跟踪训练新知探究把下列方程化成一元二次方程的一般形式，并写出它们的二次项系数、一次项系数和常数项．（1）；（2）；（3）．()224x-=()()223410xxx-+=-21132xx+-=240xx-=22140xx+-=22390xx--=1-4012-142-3-9知识点3新知探究使方程左右两边相等的未知数的值就是这个一元二次方程的解，一元二次方程的解也叫做一元二次方程的根．判断一个数值是不是一元二次方程的根的方法：将这个值代入一元二次方程，看方程的左右两边是否相等，若相等，则是方程的根；若不相等，就不是方程的根．跟踪训练新知探究1．下列哪些数是一元二次方程x2-4x+3＝0的解？-1，0，1，3．2．方程x2+x－12＝0的两个根为()A．x1＝－2，x2＝6B．x1＝－6，x2＝2C．x1＝－3，x2＝4D．x1＝－4，x2＝3D随堂练习1A．B．5x2+y=0C．ax2+bx+c=0D．(x-1)(x+2)=12321xx=+D不是整式不是一元缺少a≠0的条件下列选项中是一元二次方程的是()随堂练习2根据下列问题列方程，并将所列方程化成一元二次方程的一般形式：(1)一个圆的面积是6.28cm2，求半径；(2)一个直角三角形的两条直角边相差3cm，面积是9cm2，求较长的直角边.解：(1)设圆的半径为rcm，则圆的面积为（πr2）cm2，所以其一般形式为πr2-6.28=0．(2)设较长的直角边长为acm，则较短的直角边长为(a-3)cm，则直角三角形的面积为[a(a-3)]cm2，所以其一般形式为a2-3a-18=0．随堂练习3如果2是方程x2-c=0的一个根，那么常数c是多少？求出这个方程的其他根．解：因为2是方程x2-c=0的一个根，所以22-c=0，解得c=4，则原方程为x2-4=0，即x2=4，因为4的平方根为±2，所以方程x2-4=0的另一个根为-2．随堂练习4解：因为a为方程x2-3x+1=0的一根，所以a2-3a+1=0，则a3-4a2+4a-1=a(a2-3a+1)-(a2-3a+1)=a×0-0=0．已知a为方程x2-3x+1=0的一根，求a3-4a2+4a-1的值．课堂小结一元二次方程概念①是整式方程；②含一个未知数；（一元）③最高次数是2.（二次）一般形式ax2+bx+c=0(a≠0)其中(a≠0)是一元二次方程的必要条件；解（根）使方程左右两边相等的未知数的值.定义判断等号两边都是整式，只含一个未知数且未知数的最高次数是2的方程对接中考1若2n(n≠0)是关于x的方程x2-2mx+2n=0的根，则m-n的值为．解：因为2n(n≠0)是关于x的方程x2-2mx+2n=0的根，所以(2n)2-2m×2n+2n=0，即2n(2n-2m+1)=0，因为n≠0，所以2n-2m+1=0，化简得m-n=．对接中考2（2019·资阳中考）a是方程2x²=x+4的一个根，则代数式4a²-2a的值是.解：∵a是方程2x²=x+4的一个根，∴2a²-a=4，∴4a²-2a=2（2a²-a）=2×4=8.8对接中考3如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各剪去一个同样的小正方形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面面积是32cm2，求剪去的小正方形的边长．设剪去的小正方形的边长是xcm，根据题意可列方程为()A．10×6-4×6x=32B．(10-2x)(6-2x)=32C．(10-x)(6-x)=32D．10×6-4x2=32B