人教版--九年级上册---圆的综合应用

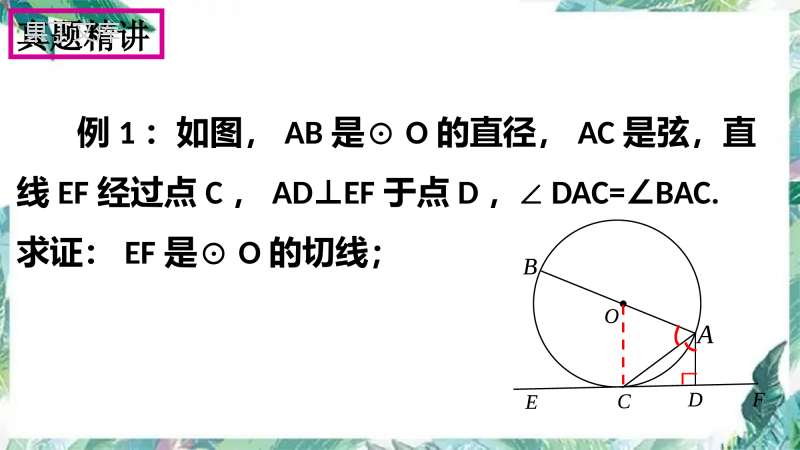
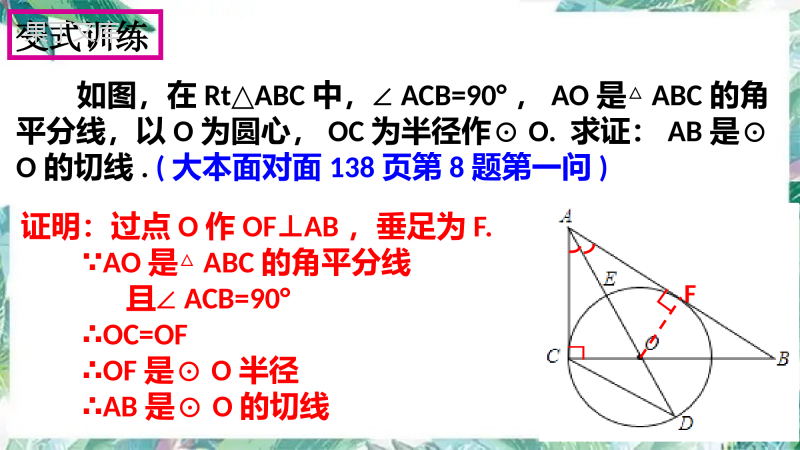
专题训练二：圆的综合应用学习目标1.掌握与切线有关的证明及计算；2.掌握解决圆综合应用题的思想与方法.学习重点掌握解决圆综合应用题的思想与方法.考点一：切线的性质及判定1.切线的性质定理：圆的切线______于过切点的半径；2.切线的判定定理：经过半径的_______并且_____于这条半径的直线是圆的切线；3.方法：①经常做的一条辅助线是：_________________;②圆中隐含条件：_____________.考点梳理垂直垂直外端作过切点的半径半径相等真题精讲例1：如图，AB是⊙O的直径，AC是弦，直线EF经过点C，ADEF⊥于点D，∠DAC=BAC.∠求证：EF是⊙O的切线；ABCDEFOABCDEFO变式训练如图，在RtABC△中，∠ACB=90°，AO是△ABC的角平分线，以O为圆心，OC为半径作⊙O.求证：AB是⊙O的切线.(大本面对面138页第8题第一问)证明：过点O作OFAB⊥，垂足为F.∵AO是△ABC的角平分线且∠ACB=90°∴OC=OF∴OF是⊙O半径∴AB是⊙O的切线F考点梳理考点二：锐角三角函数方法：①____________________；②______.考点三：相似三角形的性质与判定方法：①类似：DE²=DF·DB②求线段长度或比值考点四：勾股定理方法：用同一个量（例如半径R）表示直角三角形的三边，然后根据勾股定理列式求解.构造直角三角形转化(AA)真题精讲例2：如图，已知⊙O的直径AB与弦CD相交于点E，ABCD⊥，⊙O的切线BF与弦AD的延长线相交于点F.（1）求证：CDBF∥；（2）若⊙O的半径为5，cosC=，求线段BD的长.5454证明：（1）∵BF是⊙O的切线∴ABBF⊥∵ABCD⊥∴CDBF∥（2）∵AB是⊙O的直径∴ADBD⊥∵∠C和∠A都是弧BD所对的圆周角∴∠C=AcosA=cosC=∠∴在RtABD△中，AB=10，AD=AB·cosA=10×=8BD==6545422ADAB545422ADAB变式训练如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DEAD⊥且与AC的延长线交于点E.（1）求证：DC=DE；（2）若tanCAB=,AB=3∠，求BD的长.2121一.典型例题例1：如图，⊙O的直径AB为10cm，弦AC为6cm，ACB的平分线交⊙O于点D，求BC，AD，BD的长．ACBDOABCDO变式1:四边形是⊙O的内接四边形，与相交于点。60ABDCBDABCDACBDE（1）判断的形状。（2）若求ABC15,4,ADBADBDABCDO60ABDCBDABCDACBDEABC15,4,ADBADBDADCFBEO四边形是⊙O的内接四边形，，与相交于点，过点作⊙O切线与的延长线相交于点。60ABDCBDABCDACBDECABF（1）判断的形状。（2）若求ABC2,4CFDECDADCFBEO60ABDCBDABCDACBDECABFABC2,4CFDECDADCB二.核心模型如图CAB的平分线交⊙O于点D，CD切⊙O于点D,AC垂直CD于点C．ADCBBADCFEO中考真题如图，⊙O的直径AB，点C,D在⊙O上，且AD平分CAB，过点D作AC的垂线，与AC的延长线交于点E,与AB的延长线相交于点F.（1）求证：EF与⊙O相切；（2）若AB=6,AD=,求EF.42BADCFEO42