中考专题-与圆有关的阴影部分面积计算

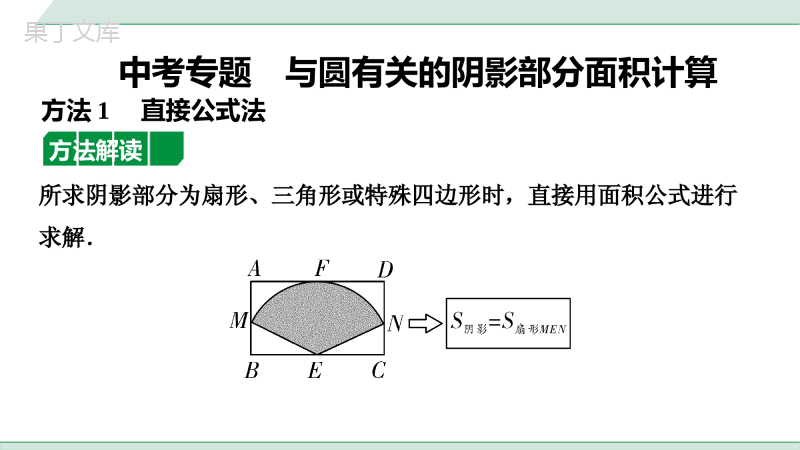
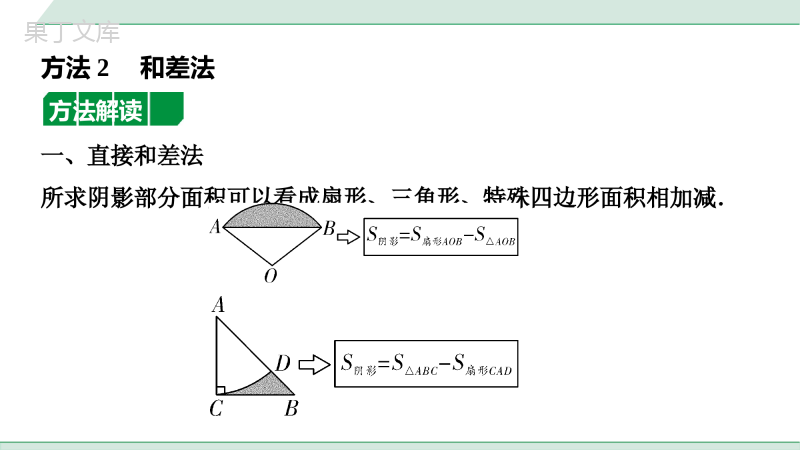
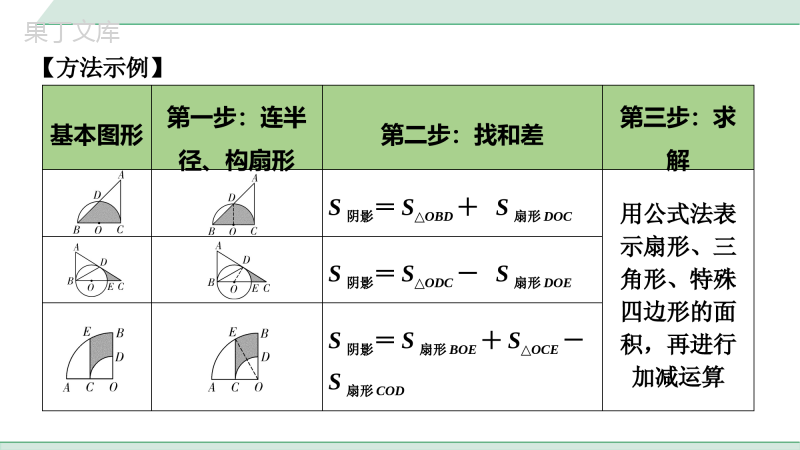
中考专题与圆有关的阴影部分面积计算所求阴影部分为扇形、三角形或特殊四边形时，直接用面积公式进行求解．方法1直接公式法方法解读1.如图，在矩形ABCD中，AB＝3，AD＝6，将AD边绕点A顺时针旋转，使点D正好落在BC边上的点D′处，则阴影部分的面积为______．2.如图，正方形ABCD的边长为1，依次以A，B，C，D为圆心，以AD，BE，CF，DG为半径画扇形，则图中四个扇形(阴影部分)的面积之和为____________．第2题图第1题图方法应用31523152一、直接和差法所求阴影部分面积可以看成扇形、三角形、特殊四边形面积相加减．方法2和差法方法解读二、构造和差法所求阴影部分面积需要添加辅助线构造扇形、三角形或特殊四边形，然后进行相加减，构造图形时一般先观察阴影部分图形：1.若阴影部分图形有一部分是弧线，找出弧线所对应的圆心，连接弧线端点与圆心构造扇形；2.若阴影部分是由图形旋转构成，旋转中心即为圆心，连接端点与旋转中心构造扇形．【方法示例】基本图形第一步：连半径、构扇形第二步：找和差第三步：求解S阴影＝S△OBD＋S扇形DOC用公式法表示扇形、三角形、特殊四边形的面积，再进行加减运算S阴影＝S△ODC－S扇形DOES阴影＝S扇形BOE＋S△OCE－S扇形COD3.如图，△ABC内接于⊙O，若∠A＝45°，⊙O的半径r＝4，则阴影部分的面积为()A.4π－8B.2πC.4πD.8π－8第3题图方法应用A4.如图，将矩形ABCD绕点A逆时针旋转90°至矩形AEFG的位置，点D的运动路径为，若AB＝2，BC＝4，则阴影部分的面积为()A.B.C.D.DG28344334233第4题图DDG283443342335.如图，在△ABC中，AC＝BC＝4，∠C＝90°，O是AB的中点，以点O为圆心，2为半径画弧分别与AC、BC相切于点D、E，与AB交于点F.则图中阴影部分的面积为________．6.(2021新乡模拟)如图，已知半圆的直径AB＝4，点C在半圆上，以点A为圆心，AC为半径画弧交AB于点D，连接BC，若∠ABC＝60°，则图中阴影部分的面积为________．第5题图第6题图32223322237.如图，在扇形AOB中，∠AOB＝90°，OA＝4，以OB为直径作半圆，圆心为点C，过点C作OA的平行线分别交两弧于点D、E，则阴影部分的面积为________．第7题图52335233通过对图形的转换，为利用公式法或和差法求解创造条件．一、直接等面积转化(CD∥AB)方法3等积转化法方法解读二、平移转化法(E、F分别为AB、CD的中点)三、对称转化法(点D为AB的中点)8.如图，AB为半圆O的直径，半径OC⊥AB.以OC为直径的⊙D交AC于点E，交BC于点F，若AB＝4，则图中阴影部分的面积为()A.π－2B.4π－2C.4π－4D.2π－2第8题图方法应用D9.如图，⊙O的半径为3，AB是⊙O的弦，过点A作⊙O的切线与OC交于点C，若OC∥AB，OC＝6，连接BC，则图中阴影部分的面积为________．10.如图，将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置，若AB＝16cm，则图中阴影部分的面积为________cm2.第9题图第10题图32323232当阴影部分是由几个图形叠加形成时，求解阴影部分面积需先找出叠加前的几个图形，然后理清图形之间的重叠关系．计算方法为：阴影部分面积＝叠加前的几个图形面积之和－(多加部分面积＋空白部分面积)．【方法示例】如图，阴影部分是扇形CAE和扇形CBD的重叠部分，则S阴影＝S扇形CAE＋S扇形CBD－S△ABC.方法4容斥原理方法解读11.如图，在矩形ABCD中，AB＝2，BC＝3，以点A为圆心，AB长为半径画弧交AD于点E，以点C为圆心，CB长为半径画弧交CD的延长线于点F，则图中阴影部分的面积为________．第11题图方法应用13641364