线性规划习题,图解法求线性规划问题

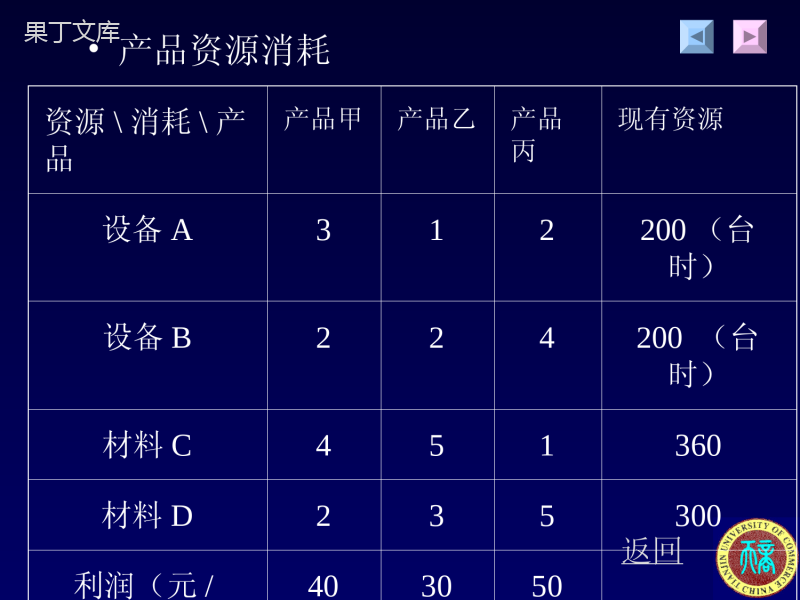
返回线性规划应用模型举例线性规划（Linearprogramming,LP）通常研究资源的优化利用、设备最佳运行等问题。例如：当任务和目标确定后，如何统筹兼顾，合理安排，用最少的资源（如：资金、设备、原材料、人工、时间等）去完成确定的任务和目标；企业在一定的资源限制下，如何组织安排生产获得最好的经济效益（如产品产量最大，利润最大）返回线性规划应用模型举例一、生产计划问题某企业在计划期内安排生产甲、乙、丙三种产品。这些产品分别需要在设备A、B上加工，需要消耗材料C、D；按工艺资料规定，单件产品在不同设备上加工及所需要的资源如表（1-1）所示。已知在计划期内设备的加工能力各为200台时，可供的材料分别为360、300公斤；每生产一件甲、乙、丙三种产品。企业可获得利润分别为40、30、50元。假定市场需求无限制，企业决策者应如何安排生产计划，使企业在计划期内总的利润最大？返回•产品资源消耗资源\消耗\产品产品甲产品乙产品丙现有资源设备A312200（台时）设备B224200（台时）材料C451360材料D235300利润（元/403050返回•解:假设在计划期内生产这三种产品的产量为xi（决策变量），Z为利润,则原问题可化为:123max403050zxxx•目标函数12312312312332200224200..4536023530001,2,3iixxxxxxstxxxxxxxxi，是整数，•约束条件返回线性规划的数学模型由决策变量、目标函数及约束条件三要素构成。•其特征是：1、解决问题的目标函数是多个决策变量的线性函数，求最大值或最小值；2、解决问题的约束条件是一组多个决策变量的线性不等式或等式；如果要求部分或全部变量是整数，则模型称为整数规划；如果目标函数或约束条件是非线性的，则模型称为非线性规划模型。返回线性规划应用模型举例二、商场值班人员安排问题营业员每周连续工作5天后连续休息2天，轮流休息。根据统计，商场每天需要的营业员如表（2）所示。商场人力资源部应该如何安排每天的上班人数，使商场总的营业员最少？返回•所需营业员数统计表星期需要人数星期需要人数一300五480二300六600三350日550四400返回•解:假设xj（决策变量）为休息两天后星期一到星期日开始上班的营业员数量，Z为商场总的营业员数,则原问题可化为:712345671minjjzxxxxxxxx•目标函数14567125671236712347123452345634567300300350400..48060055001,2,,7jjxxxxxxxxxxxxxxxxxxxxstxxxxxxxxxxxxxxxxxj，是整数，•约束条件返回线性规划应用模型举例三、合理用料问题某汽车需要用甲、乙、丙三种规格的轴各一根，这些轴的规格分别为1.5米、1米、0.7米。这些轴需要用同一种圆钢来做，圆钢长度为4米。现在要制造1000辆汽车，问：1）最少要用多少圆钢来生产这些轴？2）怎样下料使得余料最少？返回•下料方案根数方案12345678910需求量y122111000001000y210210432101000y301023012451000余料（m）00.30.50.10.400.30.60.20.5返回•解:假设yj为一根圆钢切割成甲、乙、丙三种轴的根数，xj（决策变量）为第j种下料方案所用圆钢的根数，Z为需要圆钢的根数,则原问题可化为:101minjjzx•目标函数123451346789245722100024321000..232xxxxxxxxxxxxstxxxx891045100001,2,,10jxxxxj，•约束条件返回线性规划应用模型举例四、配料问题某钢铁公司生产一种合金，要求的成分规格是：锡不少于28%，锌不少于15%，铅恰好10%，镍要界于35%~55%之间。钢铁公司拟从五种不同级别的矿石中进行冶炼，每种矿物的成分含量和价格如表。矿石杂质在冶炼的过程中废弃，求每吨合金成本最低的矿物数量？假设……？返回•矿石的金属含量矿石\合金锡锌铅镍(%)(%)(%)(%)杂质(%)费用(元/吨）125101025303402400030302603015520601804202004020230585151755190返回•解:假设xj（决策变量）为第j种矿石的数量，Z为总成本,则原问题可化为:12345min340260180230190zxxxxx•目标函数12451345135123451234512340.250.40.20.280.10.150.20.150.10.050.1..0.250.30.20.40.550.250.30.20.40.350.70.70.40.8xxxxxxxxxxxstxxxxxxxxxxxxxx5101,2,,5jxxj，•约束条件返回线性规划应用模型举例五、均衡配套生产问题某产品由2件甲零件和3件乙零件组装而成。两种零件必须在设备A、B上加工，每件甲零件在A、B上加工时间分别为5分钟和9分钟，每件乙零件在A、B上加工时间分别为4分钟和10分钟。现在2台设备A和3台设备B，每天可供加工时间为8小时。为了两种设备均衡负荷生产，要求一种设备每天的加工总时间不超过另一种设备总时间1小时。怎样安排设备的加工时间使每天产品的产量最大？返回•解:假设x1，x2（决策变量）为每天加工甲、乙两种零件的件数，y为产品的产量，则原问题可化为:1211max,min{[],[]}23zyyxx•目标函数121212125428609103860..4660,,0xxxxstxxxxy•约束条件返回•解:假设x1，x2（决策变量）为每天加工甲、乙两种零件的件数，y为产品的产量，则原问题可化为:maxzy•目标函数1212121212121[]21[]3542860..910386046604660,,0yxyxxxstxxxxxxxxy•约束条件返回线性规划应用模型举例六、投资问题某投资公司在第一年有200万资金，每年都有如下的投资方案可供考虑采纳：“假设第一年投入一笔资金，第二年又继续投入此资金的50%，那么到第三年就可回收第一年投入资金的一倍金额。”投资公司决定最优的投资策略使第六年所掌握的资金最多。返回•解:假设x1：第一年的投资x2：第一年的预留资金x3：第二年新的投资x4：第二年的预留资金x5：第三年新的投资x6：第三年的预留资金x7：第四年新的投资x8：第四年的预留资金x9：第五年的预留资金第五年不再进行投资，因为这笔投资要到第七年才能回收。约束条件保证每年满足如下的关系：追加投资金额+新投资金额+预留资金=可利用的资金总额返回12200xx第一年：（万元）13422xxxx第二年：（）+3564122xxxxx第三年：（）+5786322xxxxx第四年：（）+798522xxxx第五年：+972xx到第六年实有资金总额为：返回原问题可化为:79max2zxx•目标函数12123413456356785789200222042220..4222042200,1,2,,9jxxxxxxxxxxxstxxxxxxxxxxj•约束条件返回线性规划的一般模型：假设线性规划模型中，有m个约束条件，有n个决策变量xj(j=1,2,…,n),目标函数的变量系数用Cj表示,Cj称为价值系数。约束条件的变量系数用aij表示，aij称为工艺系数。约束条件右端的常数用bi表示，bi称为资源限量。则线性规划数学模型的一般表达式可写为：1122max(min)nnzcxcxcx•目标函数11112211211222221122((..(0,1,2,,nnnnmmmnnmjaxaxaxbaxaxaxbstaxaxaxbxjn或，）或，）或，）•约束条件返回线性规划的一般模型可简记为：1max(min)njjjzcx•目标函数1(1,2,,..0,1,2,,nijjijjaxbimstxjn或，）•约束条件返回讨论下列问题1、在例一中，假设企业一周内工作5天，每天8小时，企业设备A有5台，利用率为0.8，设备B有7台，利用率为0.85，其它条件不变，数学模型怎样变化？2、在例二中，假设Xj为工作了5后星期一到星期日开始休息的营业员数,数学模型怎样变化？3、在例三中，能否将约束条件改为等式；如果要求余料最少,数学模型怎样变化？返回讨论下列问题4、在例四中，若允许含有少量杂质，但杂质含量不超过1%，数学模型怎样变化？5、在例五中，假设同种设备的加工时间均匀分配到各台设备上，要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,数学模型怎样变化？返回•解1:假设在计划期内生产这三种产品的产量为xi（决策变量），Z为利润,一周内企业工作时间为58=40小时，设备B的一周内有效工作时间为4070.85=230台时，设备A的一周内有效工作时间为4050.8=160台时，超过题中要求的加工能力200台时，需要修改假设条件：将计划期比原来时间段延长20%，再设每天工资开销、折旧费用等为t元/天，则原问题可化为:12312312332224max403050[][]50.8870.858xxxxxxzxxxtt12312312312332200224200..4536023530001,2,3iixxxxxxstxxxxxxxxi，是整数，返回•解2:假设xj（决策变量）为假设Xj为工作了5后星期一到星期日开始休息的营业员数，Z为商场总的营业员数,则原问题可化为:712345671minjjzxxxxxxxx•目标函数23456345674567156712671237123412345300300350400..48060055001,2,,7jjxxxxxxxxxxxxxxxxxxxxstxxxxxxxxxxxxxxxxxj，是整数，•约束条件返回•解3:假设yj为一根圆钢切割成甲、乙、丙三种轴的根数，xj（决策变量）为第j种下料方案所用圆钢的根数，Z为圆钢的余料数,则原问题可化为:234578210min0.30.50.10.40.30.60.90.5zxxxxxxxx123451346789245722100024321000..232xxxxxxxxxxxxstxxxx891045100001,2,,10jxxxxj，•约束条件返回•解4:假设xj（决策变量）为第j种矿石的数量，Z为总成本,则原问题可化为:12345min340260180230190zxxxxx•目标函数12451345135123451234512340.250.40.20.280.10.150.20.150.10.050.1..0.250.30.20.40.550.250.30.20.40.350.70.70.40.8xxxxxxxxxxxstxxxxxxxxxxxxxx50.9901,2,,5jxxj，•约束条件返回•解5:假设x1，x2（决策变量）为每天加工甲、乙两种零件的件数，y为产品的产量，则原问题可化为:maxzy•目标函数•约束条件121212121212121212135428609103860..46604660549101260360,,0yxyxxxxxstxxxxxxxxxxy返回思考题1、某投资人现有下列4种投资方案，3年内每年年初都有3万元（不计利息）可供投资：方案1：在三年内投资人应在每年年初投资，一年结算一次，年收益率是20%，下一年可继续将本息投入获利；方案2：在三年内投资人应在第一年年初投资，两年结算一次，收益率是50%，下一年可继续将本息投入获利，这种投资最多不超过2万元；方案3：在三年内投资人应在第2年年初投资，两年结算一次，收益率是60%，这种投资最多不超过1.5万元；方案4：在三年内投资人应在第3年年初投资，一年结算一次，年收益率是30%，这种投资最多不超过1万元；问:投资人应采用怎样投资决策使三年的总收益最大，建立数学模型。返回思考题2、某发展公司是商务房地产开发项目的投资商.公司有机会在三个建设项目中投资:高层办公室、宾馆及购物中心，各项目不同年份所需资金和净现值见下表。三个项目的投资方案是：投资公司现在预付项目所需资金的百分比数，那么以后3年每年必须按此比例追加项目所需资金，也获得同样比例的净现值。例如，公司按10%投资项目1，现在必须支付400万，今后3年分别投入600万、900万和100万，获得净现值450万。公司目前和预计今后3年可用于三个项目的投资金额是：现有2500万，1年后2000万，2年后2000万，3年后1500万。当年没有用完的资金可以转入下一年继续使用。公司管理层希望设计一个组合投资方案，在每个项目中投资多少百分比，使其投资获得的净现值最大。返回•项目所需资金表（万元）年份项目1项目2项目30400800900160080050029008002003100700600净现值450700500返回yigch007@163.com夏英