连续型随机变量及其概率密度函数

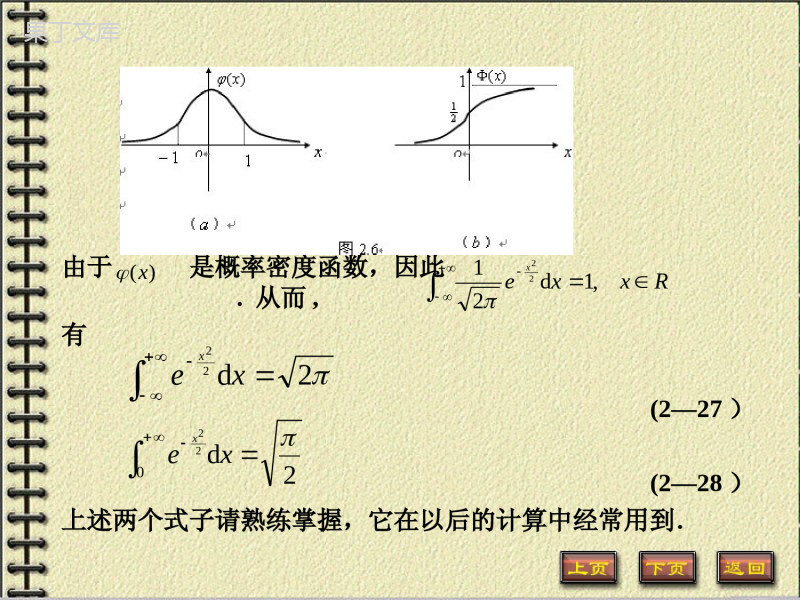
§2.4连续型随机变量及其概率密度函数一、连续型随机变量的概念定义2.8设随机变量X的分布函数为，若存在非负可积函数，使得对于任意实数，都有（2—15）则称X为连续型随机变量，称为X的概率密度函数（ProbabilityDensityFunction），简称概率密度或密度.由定义可知，连续型随机变量X的分布函数在x点的函数值等于其概率密度函数在区间上的积分．类似于离散型随机变量，连续型随机变量的概率密度函数具有如下基本性质：xFxfxxxxfxFd)()(xf)(xFxfx,xf（1）（非负性）对任意的实数，≥0；（2）（规范性）（2—16）反过来，若已知一个函数满足上述性质(1)和(2),则一定是某连续型随机变量X的概率密度函数．另外，对连续型随机变量X的分布，还具有如下性质：1.对于任意实数(),＝=；2.连续型随机变量X的分布函数是连续的,但反之不真；3.连续型随机变量X取任一确定值的概率为0；即对于任意实数，=0；事实上，由（2－12）和的连续性即知:因为连续型随机变量取任一确定值是可能的，所以,xxf1)(xxfdxfxf21,xx21xx21xXxP)()(12xFxF21)(xxxxfdxFxxXPxFxXP00xFxF（1）概率为零的事件未必是不可能事件；概率为1的事件也不一定是必然事件；（2）在计算连续型随机变量X落在某一区间的概率时，可不必区分是开区间、闭区间还是半开半闭区间，即对任意的实数，有＝＝＝＝(2—17)这样，如果除可数个点外导数处处连续,那么在的导数连续点处,而在其它点处f(x)的值可任意补充定义,不妨取为0,于是可得到X的一个概率密度函数(2－18)2121,xxxx21xXxP21xXxP21xXxP21xXxP21)(xxxxfdxFxF)(xfxF的不连续点处在，的连续点处在，)('0)(')(')(xFxFxFxf二、常见的几种连续型分布1．均匀分布定义2.9若X的概率密度函数为（2—19）则称X服从区间(a,b)内的均匀分布(UniformDistribution),记为～U(a,b)．均匀分布的特征：（1）若X～U(a,b),则落在（a,b）内任意子区间内的概率只依赖于子区间的长度，而与子区间的位置无关．事实上，对于任意一个长度的子区间,其它0),(1)(baxabxfX),(),(00balxx（2）若X～，则X的分布函数为（2－20）（3）和的图形分别为图2.3ablxabxxflxXxPlxxXPlxxlxx00001)(}{)},({0000ddbaU，bxbxaabaxaxxF，，，10)()(xf)(xF2.指数分布定义2.10若X的概率密度函数为（>0）（2—21）则称X服从参数为的指数分布(ExponentialDistribution),记为，其分布函数为(2－22）指数分布的概率密度函数和分布函数的图形分别为图2.40,00,)(xxexfx)(~EX0,00,1)(xxexFx)(xfxF生活中，指数分布应用很广．像电子元件的使用寿命、电话的通话时间、排队时所需的等待时间都可用指数分布描述．因此，指数分布在生存分析、可靠性理论和排队论中有广泛的应用．3．正态分布（1）正态分布的概念定义2.11若X的概率密度函数为（2－23）其中和为常数且，则称X服从参数为的正态分布（NormalDistribution），记为，正态分布也叫高斯分布（Gauss）,其分布函数为Rxexfx222)(21)(02,),(~2NX（2－24）特别地,当时，则称正态分布为标准正态分布,它的概率密度函数特记为，即（2—25）它的分布函数特记为，即（2—26)标准正态分布的概率密度函数和分布函数的图形分别如图2.6所示：,,d21)(222)(RxxexFxx1,0)1,0(N)(xRxexx2221)()(xxxxRxxexxxd21d)(22由于是概率密度函数，因此.从而,有(2—27）(2—28）上述两个式子请熟练掌握，它在以后的计算中经常用到．)(xRxxex,1d21222d22xex2d022xex（2）正态分布的特征若,则其概率密度函数具有如下特征：(1)的图像关于直线对称；由此便有；；(2)的最大值为；(3)愈远，值愈小,曲线以O轴为渐近线；(4)对于确定的越小，越大，X落在附近的概率越大；越大，越小，X落在附近的概率越小；(5)曲线的拐点是和),(~2NX)(xf)(xfx}{}{lXPlXP}{}{lXPXlP)(xf21)(f离xxfy)(xfx,)(f)(f)(xfy)(,f)(,f图片2.5易知:若,则.事实上,对于任意实数,的分布函数(令)所以.),(~2NX)1,0(~NXXxX}{}{}{)(xXPxuXPxXPxFxxxtexetd21d2122222xtx)1,0(~NX这样我们便有如下定理：定理2.2若，其分布函数为，则对任意实数，有（2—29）证明因为,所以.推论若，则对于任意实数，有（2－30）利用（2—30），可将一般正态分布的概率计算转化为标准正态分布的概率计算，而标准正态分布的分布函数值可由附表2获得，这样一般正态分布的概率计算就可解决．),(~2NXxFx)()(xxF),(~2NX)(}{}{}{)(xxXPxXPxXPxF),(~2NX21xx)()(}{1221xxxXxP关于标准正态分布，一个重要的公式是：对于任意实数.(2-31)这可用的定义证明或由下图说明．这里就不做证明了.图2—6另外,还有几个经常用到的公式：若X~，则对于任意实数,,()，有（1）；（2）；（3）.x1)()(xxx1,0N,x1x2x21xx)()(}{1221xxxXxP1)(2)()(}{xxxxXP)](1[2}{xxXP特别地，如果，则对任意，有，当、2、3时，分别有；；；2,~NX0k12kkXPkXP1k6826.01121XP9544.01222XP9974.01323XP可见,服从正态分布的随机变量X，虽然理论上可以取任意实数值，但实际上它的取值落在区间内的概率约为68.26%;落在区间内的概率约为95.44%,落在区间内的概率99.74%.因此,服从正态分布的随机变量X落在区间之外的概率约0.26%,还不到千分之三，这是一个小概率事件，在实际中认为它几乎不可能发生，这就是著名的“”准则．它在实际中常用来作为质量控制的依据．在自然现象和社会现象中,大量的随机变量都服从或近似服从正态分布，如，测量误差、炮弹落点距目标的偏差、海洋波浪的高度、一个地区的男性成年人的身高及体重、考试的成绩等．正是由于生活中大量的随机变量服从或近似服从正态分布，因此，正态分布在理论与实践中都占据着特别重要的地位．2,N,2,23,32,N3,33