2022-2023学年湘教版数学八年级上册同步多媒体教学-第2章-2

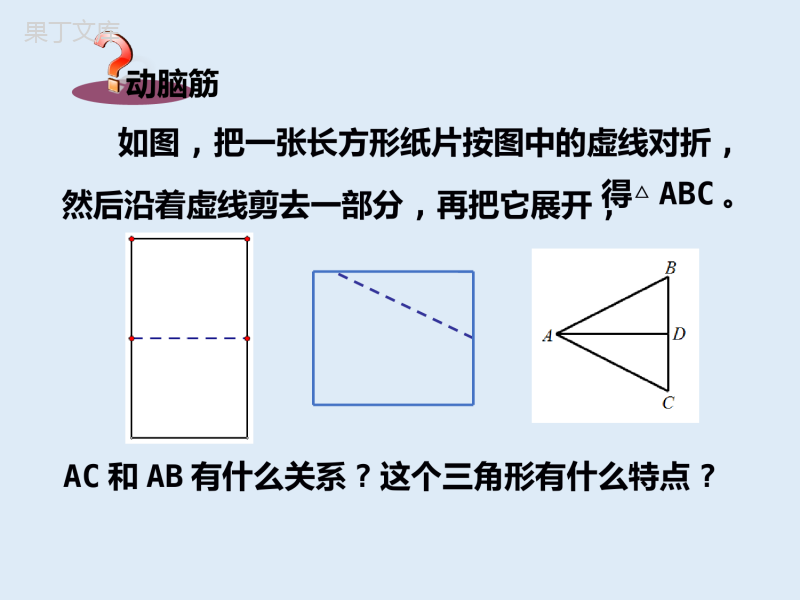
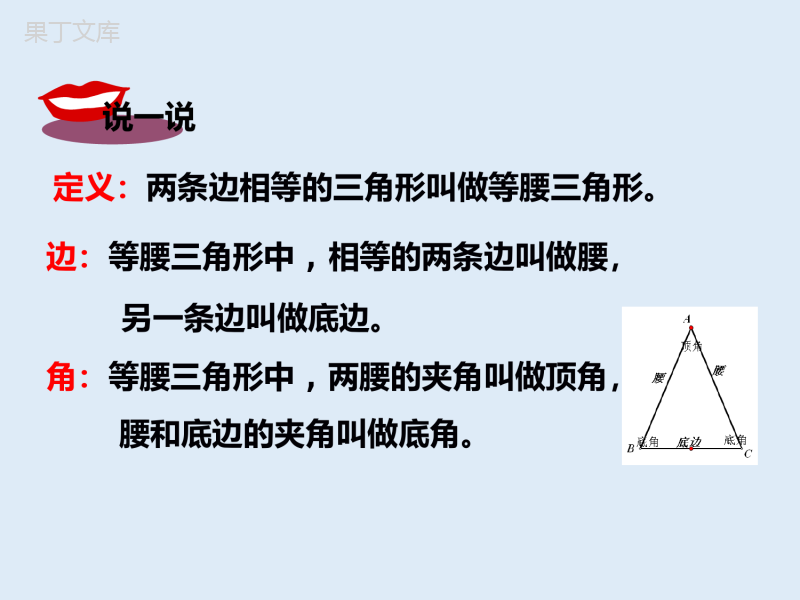
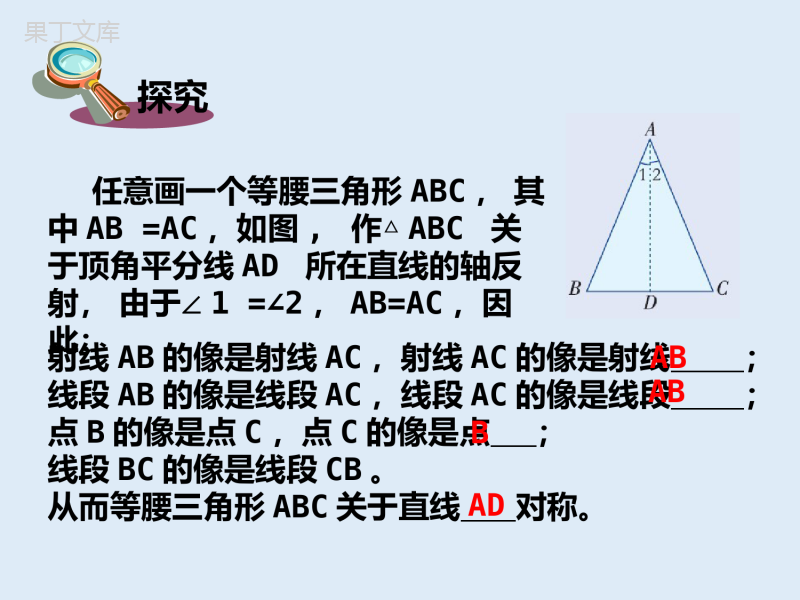
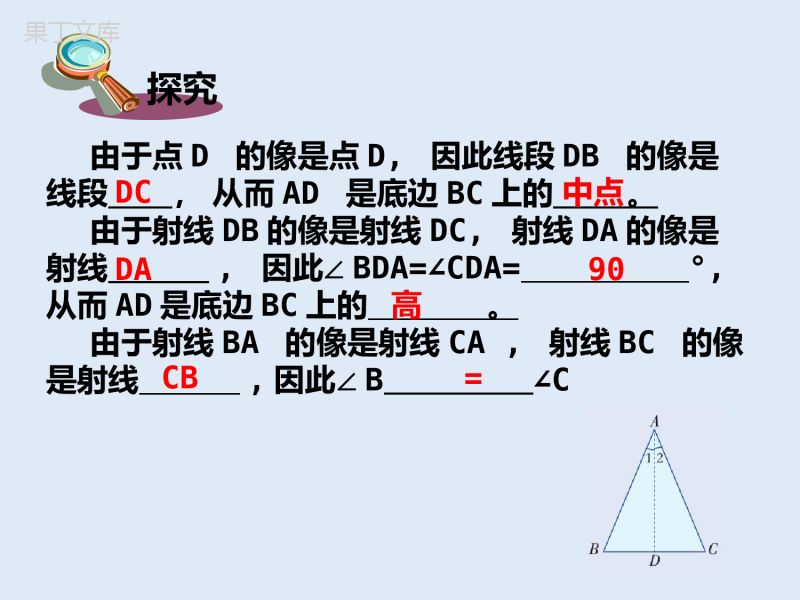
等腰三角形动脑筋如图,把一张长方形纸片按图中的虚线对折,AC和AB有什么关系?这个三角形有什么特点?然后沿着虚线剪去一部分,再把它展开,得△ABC。说一说定义：两条边相等的三角形叫做等腰三角形。边：等腰三角形中,相等的两条边叫做腰，另一条边叫做底边。角：等腰三角形中,两腰的夹角叫做顶角，腰和底边的夹角叫做底角。探究任意画一个等腰三角形ABC，其中AB=AC，如图,作△ABC关于顶角平分线AD所在直线的轴反射，由于∠1=∠2，AB=AC，因此：射线AB的像是射线AC，射线AC的像是射线；线段AB的像是线段AC，线段AC的像是线段；点B的像是点C，点C的像是点；线段BC的像是线段CB。从而等腰三角形ABC关于直线对称。ABABBAD探究由于点D的像是点D,因此线段DB的像是线段，从而AD是底边BC上的。由于射线DB的像是射线DC,射线DA的像是射线,因此∠BDA=∠CDA=°,从而AD是底边BC上的。由于射线BA的像是射线CA,射线BC的像是射线,因此∠B∠CDC中点DA90高CB=结论等腰三角形是轴对称图形，对称轴是顶角平分线所在的直线。等腰三角形的两底角相等（简称“等边对等角”）。在△ABC中，∵AC=AB（已知）∴∠B=∠C（等边对等角）几何语言：等腰三角形底边上的高、中线及顶角平分线重合（简称“三线合一”）。在△ABC中，AB=AC,点D在BC上1、∵AD⊥BC∴∠=∠，=。2、∵AD是中线，∴⊥，∠=∠。3、∵AD是角平分线，∴⊥，=。几何语言：BADCADBDCDBDCDBADCADADBCADBC在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数。解：∵在△ABC中，AB=AC∴∠ABC=∠ACB,∠A+∠ABC+∠ACB=180°∵在△ABD中，BD=AD∴∠ABD=∠A，∠BDC=∠A+∠ABD,即∠BDC=2∠A∵在△BDC中，BD=BC∴∠BDC=∠BCD,∠A+2∠ACB=180°即∠A+4∠A=180°∴∠A=36°∠ABC=∠BCA=2∠A=72°牛刀小试如图（1）在等腰△ABC中，AB=AC,∠A=36°,则∠B=,∠C=。变式练习1、如图（2）在等腰△ABC中，∠A=50°,则∠B=，∠C=。2、如图（3）在等腰△ABC中，∠A=120°则∠B=，∠C=。72°72°65°65°30°30°图（1）图（2）图（3）想一想如图，△ABC是等边三角形，那么∠A，∠B，∠C的大小之间有什么关系呢？因为△ABC是等边三角形，所以AB＝BC＝AC,从而∠C＝∠A＝∠B由三角形内角和定理可得：∠A＝∠B＝∠C＝60°等边三角形的三个内角相等，且都等于60°结论由于等边三角形是特殊的等腰三角形，因此等边三角形是轴对称图形，它有三条对称轴，分别是三个内角的平分线所在的直线。例1已知：如图,在△ABC中,AB=AC,点D,E在边BC上,且AD=AE，求证：BD=CE.证明：作AF⊥BC,垂足为点F,则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线。∴BF=CF，DF=EF，∴BF－DF=CF－EF，即BD=CE举例如图三角测平架中，AB=AC，在BC的中点D挂一个重锤，自然下垂，调整架身,使点A恰好在铅垂线上。(1)AD与BC是否垂直,试说明理由;(2)这时BC处于水平位置,为什么?议一议练习1.如图，在△ABC中，AB=AC，AD为BC边上的高，∠BAC=49°，BC=4，求∠BAD的度数及DC的长。答：∠BAD=24.5°DC=22.如图，点P为等边三角形ABC的边BC上一点，且∠APD=80°，AD=AP，求∠DPC的度数。答：∠DPC=20°中考试题1.等腰三角形两边长分别是2cm和5cm，则这个三角形周长为（）A.9cmB.12cmC.9cm或12cmD.14cmB解析另一边长为2cm或5cm，2，2，5不符合三角形三边关系定理，故选5∴周长为5+5+2=12cm中考试题2.若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角的度数为（）A.50°B.80°C.65°或50°D.50°或80°解析因为50°可作为等腰三角形的一顶角或一底角，故选DD小结与复习本节课你学习了等腰三角形的哪些重要性质?我们知道，等腰三角形的两底角相等，反过来，两个角相等的三角形是等腰三角形吗？探究如图，在△ABC中，如果∠B=∠C，那么AB与AC之间有什么关系吗？我测量后发现AB与AC相等3cm3cm事实上，如图，在△ABC中，∠B=∠C沿过点A的直线把∠BAC对折，得∠BAC的平分线AD交BC于点D，则∠1=∠2.又∠B=∠C，由三角形内角和的性质得∠ADB=∠ADC.D12沿AD所在直线折叠，由于∠ADB=∠ADC，∠1=∠2，所以射线DB与射线DC重合，射线AB与射线AC重合从而点B与点C重合，于是AB=AC结论有两个角相等的三角形是等腰三角形(简称“等角对等边”)。结论三个角都是60°的三角形是等边三角形。由此并且结合三角形内角和定理，还可以得到等边三角形的判定定理：例2已知：如图，在△ABC中，AB=AC，点D，E分别是AB，AC上的点，且DEBC∥。求证：△ADE为等腰三角形。举例证明∵AB=AC，∴∠B=∠C又∵DEBC∥，∴∠ADE=∠B，∠AED=∠C∴∠ADE=∠AED于是△ADE为等腰三角形有一个角是60°的等腰三角形是等边三角形吗？为什么？动脑筋如图，在等腰三角形ABC中，AB=AC由三角形内角和定理得∠A+∠B+∠C=180°如果顶角∠A=60°，则∠B+∠C=180°-60°=120°又AB=AC，∴∠B=∠C∴∠B=∠C=∠A=60°∴△ABC是等边三角形由此得到另一条等边三角形的判定定理：结论有一个角是60°的等腰三角形是等边三角形例3已知：如图，△ABC是等边三角形，点D，E分别在BA，CA的延长线上，且AD=AE。求证：△ADE是等边三角形。举例证明∵△ABC是等边三角形，∴∠BAC=∠B=∠C=60°∵∠EAD=∠BAC=60°又AD=AE，∴△ADE是等边三角形（有一个角是60°的等腰三角形是等边三角形）作业•谢谢