2022-2023学年湘教版数学八年级上册同步多媒体教学-第2章--三角形

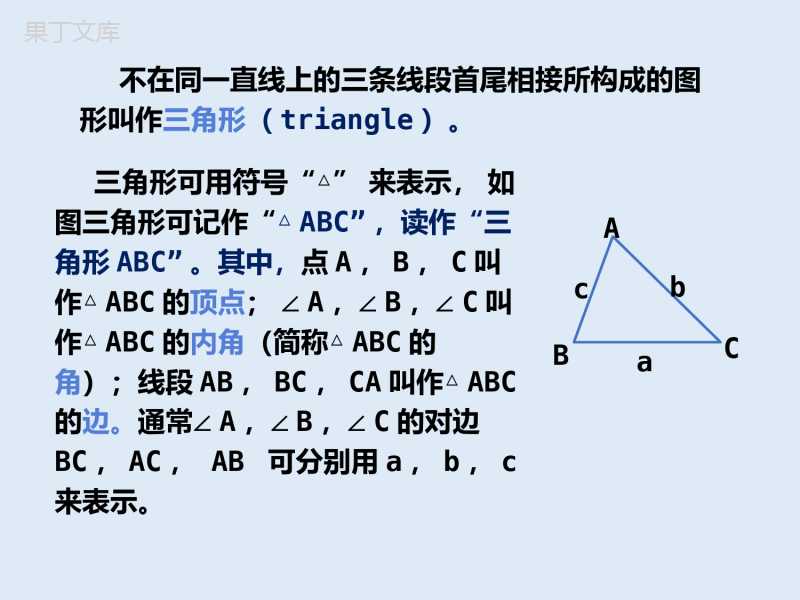
三角形三角形三角形及其相关概念观察找一找图中的三角形，并把它们勾画出来。你还能举出一些实例吗？你对小学所学的三角形内容有什么回忆？说一说三角形可用符号“△”来表示，如图三角形可记作“△ABC”，读作“三角形ABC”。其中，点A，B，C叫作△ABC的顶点；∠A，∠B，∠C叫作△ABC的内角（简称△ABC的角）；线段AB，BC，CA叫作△ABC的边。通常∠A，∠B，∠C的对边BC，AC，AB可分别用a，b，c来表示。ABCabc不在同一直线上的三条线段首尾相接所构成的图形叫作三角形（triangle）。我们如何来研究三角形？三角形如何分类呢？三角形按边如何分类呢？探究两条边相等的三角形叫作等腰三角形。在等腰三角形中，相等的两边叫作腰，另外一边叫作底边，两腰的夹角叫作顶角，腰和底边的夹角叫作底角，如右图。三边都相等的三角形叫作等边三角形（或正三角形）。等边三角形是特殊的等腰三角形—腰和底边相等的等腰三角形，如左图。ABCABC顶角等腰三角形底角底角底边腰腰等边三角形在一个三角形中，任意两边之和与第三边的长度之间有怎样的大小关系？为什么？动脑筋如图，在△ABC中，BC是连接B，C两点的一条线段，由基本事实“两点之间线段最短”可得AB+AC>BC同理可得AB+BC>AC，AC+BC>ABABCabc结论三角形的任意两边之和大于第三边.例1如图，D是△ABC的边AC上一点，AD=BD，试判断AC与BC的大小。举例ABCD解在△BDC中，有BD+DC>BC（三角形的任意两边之和大于第三边）所以AC>BC又AD=BD，则BD+DC=AD+DC=AC，练习1.（1）如图，图中有几个三角形？把它们分别表示出来.（2）如图，在△DBC中，写出∠D的对边，BD边的对角。ABCDO答：共5个.分别是△ABC,△ABO,△DBC,△DOC和△BOC答：∠D的对边是BC,BD边的对角是∠BCD。2.三根长分别为2cm，5cm，6cm的小木棒能首尾相接构成一个三角形吗？答：能构成一个三角形因为“三角形的任意两边之和大于第三边”2+5=7>6，所以能构成一个三角形.中考试题1.等腰三角形两边长分别为4和8，则这个等腰三角形的周长为()A．16B．18C．20D．16或20解析分类讨论：①当4是底边长时，周长为8+8+4=20；②当8是底边长时，周长为4+4+8=16；再由三角形的任意两边和大于第三边,确定三角形的第三边长,②不符合。C小结1.这节课我们研究的是什么？怎么研究的？2.进一步我们要研究三角形的哪些元素？三角形三角形的中线、高和角平分线请大家回忆，小学学过三角形的哪些重要线段？你对它有何认识？说一说从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫作三角形的高线（altitude），简称三角形的高。如图，AH⊥BC，垂足为点H，则线段AH是△ABC的BC边上的高。ABCH如图，试画出图中△ABC的BC边上的高.ABC做一做除了高，初中我们再介绍两种三角形的重要线段.在三角形中，一个角的平分线与这个角的对边相交，这个角的顶点与交点之间的线段叫作三角形的角平分线（angularbisector）。如图，∠BAD=∠CAD，则线段AD是△ABC的一条角平分线。ABCD在三角形中，连接一个顶点和它的对边中点的线段叫作三角形的中线（median）。如图，BD=DC，则线段AD是△ABC的BC边上的中线。ABCD任意画一个三角形，画出三边上的中线。你发现了什么？做一做事实上，三角形的三条中线相交于一点。我们把这三条中线的交点叫作三角形的重心。如图，△ABC的三条中线AD，BE，CF相交于点G，则点G为△ABC的重心。ABCDEFG例2如图，AD是△ABC的中线，AE是△ABC的高。（1）图中共有几个三角形？请分别列举出来。（2）其中哪些三角形的面积相等？解（1）图中有6个三角形，它们分别是：△ABD，△ADE，△AEC，△ABE，△ADC，△ABCABCDE举例所以（2）因为AD是△ABC的中线，所以BD=DC因为AE是△ABC的高，也是△ABD和△ADC的高，又ABDADC1122==SBDAESDCAE,,.ABDADC=SSABCDE通过反思本题第二问，你有什么发现？三角形中线把三角形平分成面积相等的两部分.练习1.利用三角尺（或直尺）、量角器任意画出一个三角形，并画出其中一条边上的中线、高以及这条边所对的角的平分线。2.如图，AD是△ABC的高，DE是△ADB的中线，BF是∠EBD的角平分线，根据已知条件填空：（1）∠ADB=∠=°；（2）BE==；（3）∠DBF=∠=∠。1212ABCDEFADC90AEABEBFEBD中考试题三角形的下列线段中能将三角形的面积分成相等两部分的是（）A.中线B.角平分线C.高D.中位线解析根据中线的定义,“连接三角形一个顶点和它对边中点的线段叫做三角形的中线”,知三角形的中线把三角形分成等底同高的两个三角形,它们的面积相等。A小结1.从知识上，在小学学习的基础上，我们又学习了什么？2.从方法上，我们是怎么认识这些重要线段的，对你后续的学习有什么启示吗？三角形三角形的性质动脑筋在小学，我们通过对一个三角形进行折叠、剪拼等操作（如图），知道三角形的内角和是180°，你能说出这些方法的原理吗？折叠三角形纸板，可以把它的三个角拼成一个角。可以将∠A，∠B剪下并移至顶点C处拼接成一个角。上述两种操作都是将三角形的三个内角拼到一起构成一个平角。因为直线在平移下的像是与它平行的直线，所以B′C′BC∥则∠B′AB＝∠B，∠C′AC＝∠C又∠B′AB+∠BAC+∠C′AC=180°所以∠B+∠BAC+∠C＝180°由此受到启发：如图，将△ABC的边BC所在的直线平移，使其像经过点A，得到直线B′C′。ABCB′C′结论三角形的内角和等于180°.三角形内角和定理还有没有别的证法呢？多种方法证明的核心是什么？借助平行线的“移角”的功能，将三个角转化成一个平角。例3在△ABC中，∠A的度数是∠B的度数的3倍，∠C比∠B大15°，求∠A，∠B，∠C的度数。解设∠B为x°，则∠A为（3x）°，∠C为（x＋15）°，从而有3x＋x＋（x＋15）＝180解得x＝33所以3x＝99，x＋15＝48答：∠A，∠B，∠C的度数分别为99°，33°，48°.举例三角形按角如何分类呢？探究一个三角形的三个内角中，最多有几个直角？最多有几个钝角？三角形的内角和等于180°，因此最多有一个直角或一个钝角.说一说三角形中，三个角都是锐角的三角形叫锐角三角形，有一个角是直角的三角形叫直角三角形，有一个角是钝角的三角形叫钝角三角形，如下图。锐角三角形直角三角形钝角三角形直角三角形可用符号“Rt△”来表示，例如直角三角形ABC可以记作“Rt△ABC”。在直角三角形中，夹直角的两边叫作直角边，直角的对边叫作斜边。两条直角边相等的直角三角形叫作等腰直角三角形。如图，把△ABC的一边BC延长，得到∠ACD。像这样，三角形的一边与另一边的延长线所组成的角，叫作三角形的外角（exteriorangle）。对外角∠ACD来说，∠ACB是与它相邻的内角，∠A，∠B是与它不相邻的内角。BCAD探究在图中，外角∠ACD和与它不相邻的内角∠A，∠B之间有什么大小关系？BAC我觉得可以利用“三角形的内角和等于180°”的结论.因为∠ACD+∠ACB=180°，∠A+∠B+∠ACB=180°，所以∠ACD-∠A-∠B=0（等量减等量，差相等）于是∠ACD=∠A+∠BD结论三角形的一个外角等于与它不相邻的两个内角的和。练习1.填空：（1）在△ABC中，∠A=60°，∠B=∠C，则∠B=；（2）在△ABC中，∠A－∠B=50°，∠C－∠B=40°，则∠B=。60°30°2.如图，AD是△ABC的角平分线，∠B=36°，∠C=76°，求∠DAC的度数。ABCD36°76°解因为∠B=36°，∠C=76°又∠BAC+∠B＋∠C=180°，因为AD是△ABC的角平分线，所以∠BAC=68°，°==3412DACBAC∠∠.所以3.如图，∠CAD＝100°，∠B＝30°，求∠C的度数。ABCD30°100°解因为∠CAD是△ABC的外角，于是∠C=∠CAD-∠B=100°-30°=70°所以∠B+∠C=∠CAD，中考试题如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=______°解析∵∠B=47°∴∠BAC+∠BCA=180°–47°=133°∴∠CAD+∠ACF=360°–133°=227°又AE和CE是角平分线，∴∠CAE+∠ACE=113.5°，∴∠E=180°66.5ABCFED小结1.这节课我们研究的是什么？为什么要这么研究？2.从方法上你有哪些收获？3.“一题多解，多解归一”，需要把多种解法的共性挖掘出来，归纳成解决一类问题的方法。作业•谢谢