2022-2023学年湘教版数学九年级上册同步多媒体教学-第3章3-4-1相似三角形的判定第4课时

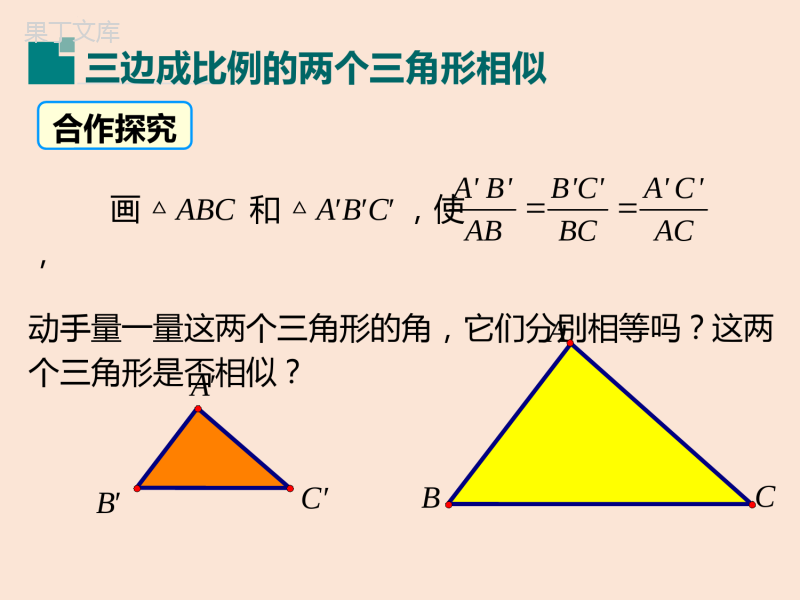
第三章图形的相似3.4.1相似三角形的判定1.复习已经学过的三角形相似的判定定理.2.掌握利用三边来判定两个三角形相似的方法，并能进行相关计算.(重点、难点)学习目标2.证明三角形全等有哪些方法？你能从中获得证明三角形相似的启发吗？1.什么是相似三角形？在前面的课程中，我们学过哪些判定三角形相似的方法？你认为这些方法是否有其缺点和局限性？ABCDE复习引入3.类似于判定三角形全等的SSS方法，我们能不能通过三边来判定两个三角形相似呢？三边成比例的两个三角形相似合作探究画△ABC和△A′B′C′，使，动手量一量这两个三角形的角，它们分别相等吗？这两个三角形是否相似？A'B'B'C'A'C'ABBCACABCC′B′A′ABCC′B′A′通过测量不难发现∠A=∠A'，∠B=∠B'，∠C=∠C'，又因为两个三角形的边对应成比例，所以△ABC∽△A′B′C′.下面我们用前面所学得定理证明该结论.∴ADDEAE.ABBCACC′B′A′证明:在线段AB(或延长线)上截取AD=A′B′，过点D作DEBC∥交AC于点E.∵DEBC∥，∴△ADE∽△ABC.∴DE=B′C′，EA=C′A′.∴△ADE≌△A′B′C′，△A′B′C′∽△ABC.BCADEA'B'B'C'A'C'ABBCAC又，AD=A′B′，∴，.DEB'C'BCBCAEA'C'ACAC由此我们得到利用三边判定三角形相似的定理：三边成比例的两个三角形相似．ACCACBBCBAAB∵，∴△ABC∽△A′B′C.符号语言：归纳总结例1如图，在Rt△ABC与Rt△A′B′C′中，∠C=∠C′=90°，且求证：Rt△A′B′C′Rt∽△ABC.ABAC.A'B'A'C'典例精析证明：设则A′B′=kAB，A′C′=kAC，∴Rt△A′B′C′Rt∽△ABC.''''''.BCABACBCABACABAC=k.A'B'A'C'∴由勾股定理，得BC2=,A′B′=,22ABAC22ABAC′′′′222222''''.''''''BCABACkABkACkBCBCBC例2判断图中的两个三角形是否相似，并说明理由．ABC33.54DFE1.82.12.4解：在△ABC中，AB>BC>CA，在△DEF中，DE>EF>FD.∴△ABC∽△DEF.ABC33.54DFE1.82.12.42.40.64DEAB∵，，，2.10.63.5EFBC1.80.63FDCADEEFFDABBCCA∴.判定三角形相似的方法之一：如果题中给出了两个三角形的三边的长，分别算出三条对应边的比值，看是否相等.注意：计算时最长边与最长边对应，最短边与最短边对应.归纳总结已知△ABC和△DEF，根据下列条件判断它们是否相似.(3)AB=12，BC=15，AC＝24，DE＝16，EF＝20，DF＝30.(2)AB=4，BC=8，AC＝10，DE＝20，EF＝16，DF＝8；(1)AB=3，BC=4，AC＝6，DE＝6，EF＝8，DF＝9；是否否练一练例3:如图,方格网的小方格是边长为1的正方形，△ABC与△A′B′C′的顶点都在格点上，△ABC与△A′B′C′相似吗?为什么?CBAA′B′C′210.510ABACBCABACBC2,2,10;ABACBC5,10,5;ABACBC解：△ABC与△A′B′C′的顶点都在格点上，根据勾股定理，得△△ABC与△A′B′C′相似.∴∠BAC=∠DAE，∠BAC－∠DAC=∠DAE－∠DAC，即∠BAD=∠CAE.∵∠BAD=20°，∴∠CAE=20°.∴△ABC∽△ADE(三边成比例的两个三角形相似).例4如图，在△ABC和△ADE中，∠BAD=20°，求∠CAE的度数..ABBCACADDEAEABCDEABBCACADDEAE，解：∵解：在△ABC和△ADE中，∵AB:CD=BC:DE=AC:AE，∴△ABC∽△ADE，∴∠BAC=∠DAE，∠B=∠D，∠C=∠E.∴∠BAC－∠CAD=∠DAE－∠CAD，∴∠BAD=∠CAE.故图中相等的角有∠BAC=∠DAE，∠B=∠D，∠C=∠E，∠BAD=∠CAE.如图，已知AB:AD=BC:DE=AC:AE，找出图中相等的角(对顶角除外)，并说明你的理由.练一练ABCDE1.如图，若△ABC∽△DEF，则x的值为()ABCDEFA.20B.27C.36D.45C2.如图，在大小为4×4的正方形网格中，是相似三角形的是()①②③④A.①和②B.②和③C.①和③D.②和④C3.如图，∠APD=90°，AP=PB=BC=CD，下列结论正确的是()A.△PAB∽△PCAB.△PAB∽△PDAC.△ABC∽△DBAD.△ABC∽△DCAACBPDC∵AB:BC=BD:AB=AD:AC，∴△ABC∽△DBA，故选C.解析：设AP=PB=BC=CD=1，∵∠APD=90°，∴AB=，AC=，AD=.25104.根据下列条件，判断△ABC与△A′B′C′是否相似：AB=4cm，BC=6cm，AC=8cm，A′B′=12cm，B′C′=18cm，A′C′=21cm.答案：不相似.5.如图，△ABC中，点D，E，F分别是AB，BC，CA的中点，求证：△ABC∽△EFD．∴△ABC∽△EFD.证明：∵△ABC中，点D，E，F分别是AB，BC，CA的中点，∴111=222DEACDFBCEFAB，，，∴1=2DEDFEFACBCAB=，6.如图，某地四个乡镇A，B，C，D之间建有公路，已知AB=14千米，AD=28千米，BD=21千米，DC=31.5千米，公路AB与CD平行吗？说出你的理由.ACBD2814214231.5解：公路AB与CD平行.∴2=3ABADBDBDBCDC=，∴△ABD∽△BDC，∴∠ABD=∠BDC，∴ABDC∥.三边成比例的两个三角形相似利用三边判定两个三角形相似相似三角形的判定定理的运用谢谢观看