人教版七年级上册数学有理数的乘方第一课时

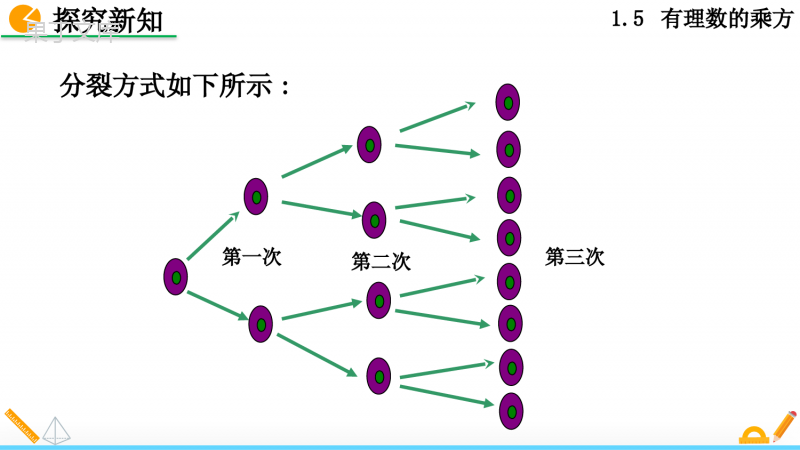
1.5有理数的乘方1.5有理数的乘方1.5.1乘方（第1课时）人教版数学七年级上册1.5有理数的乘方珠穆朗玛峰是世界最高的山峰，它的海拔高度约是8844米．把一张足够大的厚度为0.1毫米的纸，连续对折30次的厚度能超过珠穆朗玛峰，这是真的吗？导入新知1.5有理数的乘方素养目标1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义.2.体会有理数乘方运算的符号法则，熟练进行有理数的乘方运算.1.5有理数的乘方某种细胞每30分钟便由一个分裂成两个，经过3小时这种细胞由1个能分裂成多少个？乘方的意义知识点探究新知1.5有理数的乘方探究新知第一次第二次第三次分裂方式如下所示:1.5有理数的乘方这个细胞分裂一次可得多少个细胞?那么，3小时共分裂了多少次?有多少个细胞？解:一次：两次：三次：四次：2个；2×2个；2×2×2个；六次:2×2×2×2×2×2个.分裂两次呢?分裂三次呢?四次呢？【思考】2×2×2×2个；探究新知1.5有理数的乘方请比较细胞分裂四次后的个数式子:2×2×2×2和细胞分裂六次后的个数式子:2×2×2×2×2×2.这两个式子有什么相同点?它们都是乘法，并且它们各自的因数都相同.【想一想】这样的运算能像平方、立方那样简写吗？探究新知1.5有理数的乘方一般地，n个相同的因数a相乘，记作an，读作“a的n次幂（或a的n次方）”，即a·a·a··a=ann个…探究新知例如：2×2×2×2422×2×2×2×2×262记作记作读作2的6次方(幂).读作2的4次方(幂).42621.5有理数的乘方这种求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂.na幂指数因数的个数底数因数一个数可以看作这个数本身的一次方，例如，8就是81，指数1通常省略不写.因为an就是n个a相乘，所以可以利用有理数的乘法运算来进行有理数的乘方运算.探究新知na1.5有理数的乘方1.(–5)2的底数是_____，指数是_____，(–5)2表示2个_____相乘，读作_____的2次方，也读作–5的_____.2.表示个相乘，读作的次方，也读作的次幂，其中叫做，6叫做.612温馨提示：幂的底数是分数或负数时，底数应该添上括号！12121212–52–5–5平方666底数指数探究新知【试一试】612121212121.5有理数的乘方323（1）(–4)3；（2）(–2)4；（3）.例1计算：解：（1）(–4)3=(–4)×(–4)×(–4)=–64；（2）(–2)4=(–2)×(–2)×(–2)×(–2)=16；.322228333327你发现负数的幂的正负有什么规律？素养考点1乘方的计算探究新知（3）323.3222283333271.5有理数的乘方1.负数的奇次幂是负数，负数的偶次幂是正数.2.正数的任何正整数次幂都是正数，0的任何正整数次幂都是0.根据有理数的乘法法则可以得出：探究新知归纳总结1.5有理数的乘方（4）；()422222（）（）（）（）判断：(对的画“√”，错的画“×”.)（1）32=3×2=6；()（2）(–2)3＝(–3)2；()（3）–32=(–3)2；()（5）.()222233×32=3×3=9(–2)3＝–8；(–3)2=9–32=–9；(–3)2=9–24=–2×2×2×2=–16××××22439巩固练习422222（）（）（）（）222233224391.5有理数的乘方例2用计算器计算(–8)5和(–3)6.解：用带符号键的计算器.(–)=)(–)(＜85显示：(–8)5＜–32768.=)(–)(＜36显示：(–3)6＜729.所以(–8)5=–32768，(–3)6=729.素养考点2利用计算器进行乘方的计算探究新知1.5有理数的乘方用计算器计算：（1）=_________（2）=___________（3）=_________（4）=__________()61171638.43(5.6)1771561592.704268435456–175.616若运用初中数学教材中使用的某种电子计算器进行计算，则按键的结果为()A.16B.33C.37D.36B巩固练习()61171638.43(5.6)1.5有理数的乘方例3计算（1）（2）–23×(–32)（3）64÷(–2)5（4）(–4)3÷(–1)200+2×(–3)422-3-3（）（）含有乘方的运算素养考点3探究新知22(-3)(-)329(-)6;3（2）–23×(–32)=–8×(–9)=72；（3）64÷(–2)5=64÷(–32)=–2；（4）(–4)3÷(–1)200+2×(–3)4=–64÷1+2×81=98解：（1）22-3-3（）（）22(-3)(-)329(-)6;31.5有理数的乘方【思考】通过以上计算，对于乘除和乘方的混合运算，你觉得有怎样的运算顺序？先算乘方，后算乘除；如果遇到括号，就先进行括号里的运算.探究新知1.5有理数的乘方计算:（1）–0.252÷(–)4×(–1)27（2）(–2)5×（）3×(–1)2015（3）–2×3–(–2×3)21212解：（1）原式＝=1（2）原式＝=4（3）原式＝–2×3–36=–42巩固练习2412(1)4531(2)(1)212122412(1)4531(2)(1)21.5有理数的乘方1.计算(–3)2等于（）A．5B．–5C．9D．–92.计算(–1)2017的结果是（）A.–1B.1C.2017D.–2017CA连接中考1.5有理数的乘方1.填空：（1）–(–3)2=;（2）–32=;（3）(–5)3=;（4）0.13=;（5）(–1)9=;（6）(–1)12=;（7）(–1)2n=;（8）(–1)2n+1=;（9）(–1)n=.–9–9–1250.001–111–1-11（当n为奇数时）（当n为偶数时）基础巩固题课堂检测-111.5有理数的乘方2.计算：.课堂检测211(6)()23解：原式==18-12=61136()233.下列说法中正确的是（）A.23表示2×3的积B.任何一个有理数的偶次幂是正数C.-32与(-3)2互为相反数D.一个数的平方是，这个数一定是4923C211(6)()231136()2349231.5有理数的乘方2.对任意实数a，下列各式不一定成立的是（）BB能力提升题课堂检测1.在中，最大的数是()––33，–(–3)3，(–3)3，–33A.––33B.–(–3)3C.(–3)3D.–33A.a2=(–a)2B.a3=(–a)3C.a=–aD.a2≥01.5有理数的乘方厚度是0.1毫米的纸,将它对折1次后,厚度为0.2毫米.（1）对折3次后,厚度为多少毫米?（2）对折7次后,厚度为多少毫米?（3）用计算器计算对折30次后纸的厚度.0.1×230=0.1×1073741824=107374182.4（毫米）＞8848米107374182.4毫米=107374.1824米拓广探索题课堂检测0.8毫米12.8毫米.1.5有理数的乘方1.求几个相同因数的积的运算，叫做乘方.2.乘方的符号法则：（1）正数的任何次幂都是正数.（2）负数的奇次幂是负数，负数的偶次幂是正数.（3）零的正整数次幂都是零.na幂指数底数课堂小结na1.5有理数的乘方课后作业作业内容教材作业从课后习题中选取自主安排配套练习册练习